题目内容
【题目】某河道中过度滋长一种藻类,环保部门决定投入生物净化剂净化水体. 因技术原因,第t分钟内投放净化剂的路径长度![]() (单位:m),净化剂净化水体的宽度
(单位:m),净化剂净化水体的宽度![]() (单位:m)是时间t(单位:分钟)的函数:
(单位:m)是时间t(单位:分钟)的函数: ![]() (
(![]() 由单位时间投放的净化剂数量确定,设
由单位时间投放的净化剂数量确定,设![]() 为常数,且
为常数,且![]() ).
).
(1)试写出投放净化剂的第t分钟内净化水体面积![]() 的表达式;
的表达式;
(2)求![]() 的最小值.
的最小值.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)根据题意去掉绝对值写出分段函数的表达式;(2)当40≤t≤60且t∈N*时,S(t)= ![]() 在40≤t≤60时单调递减;当t=60时,S(t)有最小值2a2+120.当1≤t<40且t∈N*时,S(t)=
在40≤t≤60时单调递减;当t=60时,S(t)有最小值2a2+120.当1≤t<40且t∈N*时,S(t)= ![]() ≥100+a2+20a;①若a=1或2或3时 S(t)在1≤t<40范围中有最小值a2+2a +100.在40≤t≤60时S(t)有最小值2a2+120.当a=1时,100+a2+20a=121<122=2a2+120,故S(t)有最小值121;当a=2或a=3时,100+a2+20a>2a2+120,故S(t)有最小值2a2+120.②若a≥4且1≤t<40时, S(t+1)=100+a2+t+1+
≥100+a2+20a;①若a=1或2或3时 S(t)在1≤t<40范围中有最小值a2+2a +100.在40≤t≤60时S(t)有最小值2a2+120.当a=1时,100+a2+20a=121<122=2a2+120,故S(t)有最小值121;当a=2或a=3时,100+a2+20a>2a2+120,故S(t)有最小值2a2+120.②若a≥4且1≤t<40时, S(t+1)=100+a2+t+1+![]() ≤S(t)=100+a2+t+
≤S(t)=100+a2+t+![]() , S(t)在1≤t≤60时单调递减.当t=60时,S(t)有最小值2a2+120.
, S(t)在1≤t≤60时单调递减.当t=60时,S(t)有最小值2a2+120.
试题解析:(1)由题意, 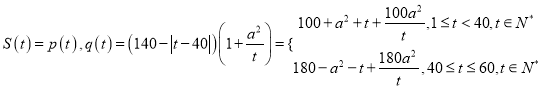 .
.
(2)当40≤t≤60且t∈N*时,S(t)= ![]() ,当t增加时
,当t增加时![]() 减少,
减少,
所以S(t)在40≤t≤60时单调递减;当t=60时,S(t)有最小值2a2+120.
当1≤t<40且t∈N*时,S(t)= ![]() ≥100+a2+20a;
≥100+a2+20a;
①若a=1或2或3时;当t=10a时,上述不等式中的等号成立,
S(t)在1≤t<40范围中有最小值a2+2a +100.
又在40≤t≤60时S(t)有最小值2a2+120.
当a=1时,100+a2+20a=121<122=2a2+120,故S(t)有最小值121;
当a=2或a=3时,100+a2+20a>2a2+120,故S(t)有最小值2a2+120.
②若a≥4且1≤t<40时,因为![]() ≤0,
≤0,
所以S(t+1)=100+a2+t+1+![]() ≤S(t)=100+a2+t+
≤S(t)=100+a2+t+![]() ,
,
故S(t)在1≤t≤40中单调递减;又S(t)在40≤t≤60时单调递减,
所以S(t)在1≤t≤60时单调递减.
所以,当t=60时,S(t)有最小值2a2+120.
综上,若a=1,当t=10时,S(t)有最小值121;即第10天的销售额最少,为121千元.
若a≥4且a∈N*,当t=60时,S(t)有最小值2a2+120.