题目内容
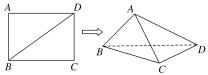
【题目】如图,在长方体ABCDA1B1C1D1中,AB=AA1=1,E为BC中点.
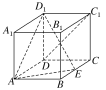
(1)求证:C1D⊥D1E;
(2)在棱AA1上是否存在一点M,使得BM∥平面AD1E?若存在,求![]() 的值,若不存在,说明理由;
的值,若不存在,说明理由;
(3)若二面角B1AED1的大小为90°,求AD的长.
【答案】见解析
【解析】解:(1)证明:以D为坐标原点,建立如图所示的空间直角坐标系Dxyz,
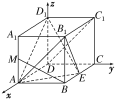
设AD=a,则D(0,0,0),A(a,0,0),B(a,1,0),B1(a,1,1),C1(0,1,1),D1(0,0,1),E![]() ,∴
,∴![]() =(0,-1,-1),
=(0,-1,-1),![]() =
=![]() ,
,
![]() ∴C1D⊥D1E。
∴C1D⊥D1E。
(2)设![]() =h,则M(a,0,h),
=h,则M(a,0,h),
∴![]() =(0,-1,h),
=(0,-1,h),![]() =
=![]() ,
,![]() =(-a,0,1),
=(-a,0,1),
设平面AD1E的法向量为n=(x,y,z),
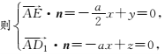
∴平面AD1E的一个法向量为n=(2,a,2a),
∵BM∥平面AD1E,
∴![]() ⊥n,即
⊥n,即![]() ·n=2ah-a=0,∴h=
·n=2ah-a=0,∴h=![]() 。
。
即在AA1上存在点M,使得BM∥平面AD1E,此时![]() =
=![]() 。
。
(3)连接AB1,B1E,设平面B1AE的法向量为m=(x′,y′,z′),![]() =
=![]() ,
,![]() =(0,1,1),
=(0,1,1),
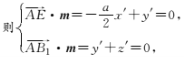
∴平面B1AE的一个法向量为m=(2,a,-a).
∵二面角B1AED1的大小为90°,
∴m⊥n,∴m·n=4+a2-2a2=0,
∵a>0,∴a=2,即AD=2。

练习册系列答案
相关题目