题目内容
如图，正三棱锥ABCD内接于球O，底面边长为
，侧棱长为2，则球O的表面积为（ ）
A．
B．
C．
D．
【答案】分析：由题意推出球心O到四个顶点的距离相等，利用直角三角形BOE，求出球的半径，即可求出外接球的表面积．
解答：
解：∵正三棱锥P-ABC中，底面边长为 
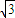，侧棱长为2，高AE=
得到球心O到四个顶点的距离相等，
在直角三角形BOE中
BO=R，EO=
-R，BE=1，
由BO2=BE2+EO2得R=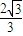
∴外接球的半径为
，表面积为：
．
故选C．
点评：本题是基础题，考查空间想象能力，计算能力；直角三角形BOE是本题解题的关键，仔细观察和分析题意，是解好数学题目的前提．
解答：
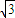解：∵正三棱锥P-ABC中，底面边长为 ，侧棱长为2，高AE=得到球心O到四个顶点的距离相等，
在直角三角形BOE中
BO=R，EO=
-R，BE=1，由BO2=BE2+EO2得R=
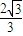
∴外接球的半径为
，表面积为：．故选C．
点评：本题是基础题，考查空间想象能力，计算能力；直角三角形BOE是本题解题的关键，仔细观察和分析题意，是解好数学题目的前提．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
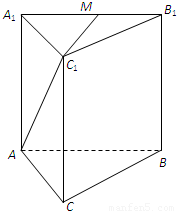
如图，正三棱锥ABC-A1B1C1的底面边长为a，侧棱长为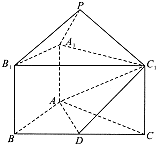
如图，正三棱锥ABC-A1B1C1中，AB=2，AA1=1，D是BC的中点，点P在平面BCC1B1内，PB1=PC1=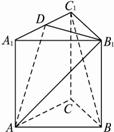
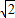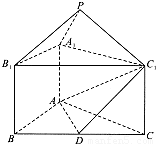
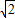，若经过对角线AB1且与对角线BC1平行的平面交上底面于DB1.
．
a，M是A1B1的中点．
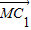是平面ABB1A1的一个法向量；