题目内容
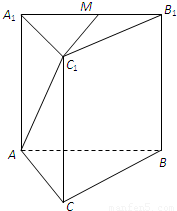
如图,正三棱锥ABC—A1B1C1中,底面边长为a,侧棱长为
(1)试确定D点的位置,并证明你的结论;
(2)求平面AB1D与侧面AB1所成的角及平面AB1D与底面所成的角;
(3)求A1到平面AB1D的距离.
解析:(1)D为A1C1的中点,连结A1B与AB1交于E,则E为A1B的中点,DE为平面AB1D与平面A1BC1的交线,?
∵BC1∥平面AB1D,BC1∥DE,?
∴D为A1C1的中点.?
(2)过D作DF⊥A1B1于F,由正三棱锥的性质,AA1⊥DF,∴DF⊥平面AB1.?
连结DG,则∠DGF为平面AB1D与侧面AB1所成的角的平面角,可求得DF=![]() a.?
a.?
由△B1FG≌△B1AA1,得FG=![]() a.?
a.?
∴∠DGF=![]() .?
.?
∵D为A1C1的中点,∴B1D⊥A1C1.?
由正三棱锥的性质,AA1⊥B1D.?
∴B1D⊥平面A1C.∴B1D⊥AD.?
∴∠A1DA是平面AB1D与上底面所成的角的平面角,可求得tan∠A1DA=![]() ,?
,?
∴∠A1DA=arctan![]() .?
.?
(3)过A1作A1M⊥AD,∵B1D⊥平面A1C,∴B1D⊥A1M.∴A1M⊥平面AB1D,即A1M是A1到平面AB1D的距离.AD=![]() a,∴A1M=
a,∴A1M=![]() a.
a.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
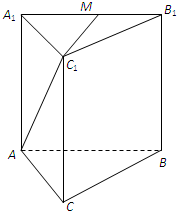 如图,正三棱锥ABC-A1B1C1的底面边长为a,侧棱长为
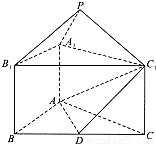
如图,正三棱锥ABC-A1B1C1的底面边长为a,侧棱长为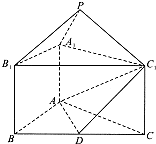 如图,正三棱锥ABC-A1B1C1中,AB=2,AA1=1,D是BC的中点,点P在平面BCC1B1内,PB1=PC1=
如图,正三棱锥ABC-A1B1C1中,AB=2,AA1=1,D是BC的中点,点P在平面BCC1B1内,PB1=PC1=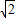 .
.
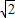 a,M是A1B1的中点.
a,M是A1B1的中点.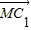 是平面ABB1A1的一个法向量;
是平面ABB1A1的一个法向量;