题目内容
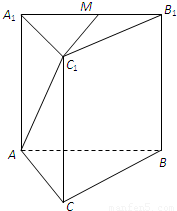
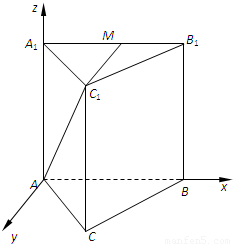
如图,正三棱锥ABC-A1B1C1的底面边长为a,侧棱长为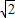 a,M是A1B1的中点.
a,M是A1B1的中点.(I)求证:
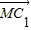 是平面ABB1A1的一个法向量;
是平面ABB1A1的一个法向量;(II)求AC1与侧面ABB1A1所成的角.
【答案】分析:(I)以点A为坐标原点,平面ABC为xoy平面,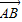 方向为x轴正方向,建立空间直角坐标系,利用向量法能够证明
方向为x轴正方向,建立空间直角坐标系,利用向量法能够证明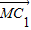 是平面ABB1A1的一个法向量;
是平面ABB1A1的一个法向量;
(II)由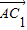 =
=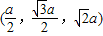 ,
,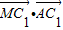 =
= ,
,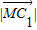 =
=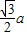 ,
,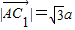 ,能够求出AC1与侧面ABB1A1所成的角.
,能够求出AC1与侧面ABB1A1所成的角.
解答:解:(I)如图,以点A为坐标原点,平面ABC为xoy平面,
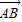 方向为x轴正方向,建立空间直角坐标系,
方向为x轴正方向,建立空间直角坐标系,
则A(0,0,0),B(a,0,0),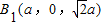 ,
,
M(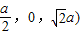 ,
,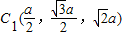
所以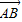 =(a,0,0),
=(a,0,0),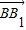 =
=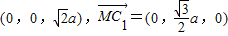 .…(5分)
.…(5分)
因为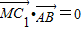 ,
, ,
,
所以MC1⊥AB,MC1⊥BB1,
从而MC1⊥平面ABB1A1.
故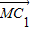 是平面ABB1A1的一个法向量.…(9分)
是平面ABB1A1的一个法向量.…(9分)
(II)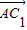 =
=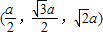 .
.
因为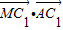 =
=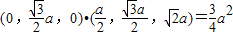 ,
,
又因为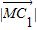 =
=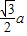 ,
,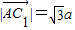 ,
,
所以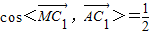 ,即
,即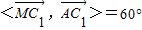 .…(13分)
.…(13分)
故AC1与侧面ABB1A1所成的角为30°.…(14分)
点评:本题考查平面的法向量的证明,考查直线与平面所成角的大小的求法.解题时要认真审题,仔细解答,注意向量法的合理运用.
 方向为x轴正方向,建立空间直角坐标系,利用向量法能够证明
方向为x轴正方向,建立空间直角坐标系,利用向量法能够证明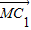 是平面ABB1A1的一个法向量;
是平面ABB1A1的一个法向量;(II)由
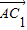 =
=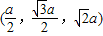 ,
,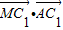 =
= ,
,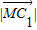 =
=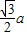 ,
,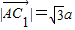 ,能够求出AC1与侧面ABB1A1所成的角.
,能够求出AC1与侧面ABB1A1所成的角.解答:解:(I)如图,以点A为坐标原点,平面ABC为xoy平面,
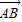 方向为x轴正方向,建立空间直角坐标系,
方向为x轴正方向,建立空间直角坐标系,则A(0,0,0),B(a,0,0),
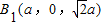 ,
,M(
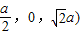 ,
,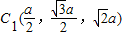

所以
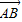 =(a,0,0),
=(a,0,0),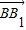 =
=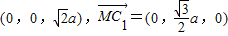 .…(5分)
.…(5分)因为
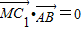 ,
, ,
,所以MC1⊥AB,MC1⊥BB1,
从而MC1⊥平面ABB1A1.
故
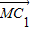 是平面ABB1A1的一个法向量.…(9分)
是平面ABB1A1的一个法向量.…(9分)(II)
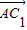 =
=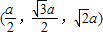 .
.因为
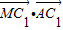 =
=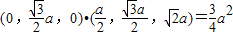 ,
,又因为
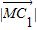 =
=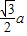 ,
,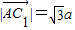 ,
,所以
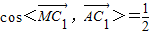 ,即
,即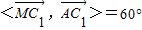 .…(13分)
.…(13分)故AC1与侧面ABB1A1所成的角为30°.…(14分)
点评:本题考查平面的法向量的证明,考查直线与平面所成角的大小的求法.解题时要认真审题,仔细解答,注意向量法的合理运用.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
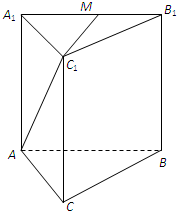 如图,正三棱锥ABC-A1B1C1的底面边长为a,侧棱长为
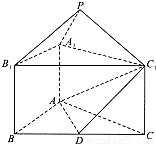
如图,正三棱锥ABC-A1B1C1的底面边长为a,侧棱长为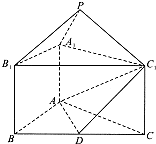 如图,正三棱锥ABC-A1B1C1中,AB=2,AA1=1,D是BC的中点,点P在平面BCC1B1内,PB1=PC1=
如图,正三棱锥ABC-A1B1C1中,AB=2,AA1=1,D是BC的中点,点P在平面BCC1B1内,PB1=PC1=
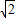 .
.