题目内容
与曲线
+
=1共焦点,而与曲线
-
=1共渐近线的双曲线方程为( )
| x2 |
| 24 |
| y2 |
| 49 |
| x2 |
| 36 |
| y2 |
| 64 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:根据椭圆方程先求出焦点坐标,再由渐近线相同设出双曲线方程为
-
=λ(λ<0),根据c值列出方程求出λ的值即可.
| x2 |
| 36 |
| y2 |
| 64 |
解答:
解:由题意得,曲线
+
=1是焦点在y轴上的椭圆,且c=
=
=5,
所以双曲线焦点的坐标是(0、5)、(0,-5),
因为双曲线与曲线
-
=1共渐近线,所以设双曲线方程为
-
=λ(λ<0),
即
-
=1,则-64λ-36λ=25,解得λ=-
,
所以双曲线方程为
-
=1,
故选:A.
| x2 |
| 24 |
| y2 |
| 49 |
| a2-b2 |
| 49-24 |
所以双曲线焦点的坐标是(0、5)、(0,-5),
因为双曲线与曲线
| x2 |
| 36 |
| y2 |
| 64 |
| x2 |
| 36 |
| y2 |
| 64 |
即
| y2 |
| -64λ |
| x2 |
| -36λ |
| 1 |
| 4 |
所以双曲线方程为
| y2 |
| 16 |
| x2 |
| 9 |
故选:A.
点评:本题考查渐近线相同的双曲线方程设法,以及椭圆、双曲线的基本量的关系,属于中档题.

练习册系列答案
相关题目
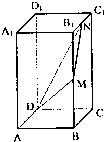 如图,在长方体ABCD-A1B1C1D1中,M、N分别为BB1、B1C1的中点,P为平面DMN内的一动点,若点P到平面BCC1B1的距离等于PD时,则点的轨迹是( )
如图,在长方体ABCD-A1B1C1D1中,M、N分别为BB1、B1C1的中点,P为平面DMN内的一动点,若点P到平面BCC1B1的距离等于PD时,则点的轨迹是( )| A、圆或圆的一部分 |
| B、抛物线的一部分 |
| C、双曲线的一部分 |
| D、椭圆的一部分 |
若椭圆2kx2+ky2=1的一个焦点坐标是(0,4),则k的值为( )
A、
| ||
B、
| ||
| C、2 | ||
D、
|
某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为y1=5.06x-0.15x2和y2=2x,其中x为销售量(单位:辆),若该公司在这两地共销售15辆车,则能获得的最大利润为( )
| A、45.6万元 |
| B、45.606万元 |
| C、45.56万元 |
| D、45.51万元 |
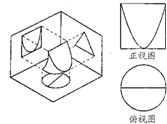 一个圆柱从顶部切掉两块,剩下部分几何体如图所示,此几何体的正视图和俯视图如图所示,其中正视图中的四边形是边长为2的正方形,则此几何体的侧视图的面积为( )
一个圆柱从顶部切掉两块,剩下部分几何体如图所示,此几何体的正视图和俯视图如图所示,其中正视图中的四边形是边长为2的正方形,则此几何体的侧视图的面积为( )