题目内容
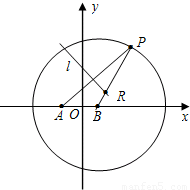
在平面直角坐标系xOy中,已知圆B:(x-1)2+y2=16与点A(-1,0),P为圆B上的动点,线段PA的垂直平分线交直线PB于点R,点R的轨迹记为曲线C.(1)求曲线C的方程;
(2)曲线C与x轴正半轴交点记为Q,过原点O且不与x轴重合的直线与曲线C的交点记为M,N,连接QM,QN,分别交直线x=t(t为常数,且t≠2)于点E,F,设E,F的纵坐标分别为y1,y2,求y1•y2的值(用t表示).
【答案】分析:(1)利用线段的垂直平分线的性质和椭圆的定义即可得出;
(2)设M(x,y),则N(-x,-y),由Q(2,0),可分别表示出QM,QN的斜率,利用点斜式即可得到直线QM,QN的方程,进而即可得到点E,F的纵坐标,再利用点M,N在椭圆上,满足椭圆的方程即可得出.
解答:解:(1)连接RA,由题意得,|RA|=|RP|,|RP|+|RB|=4,
∴|RA|+|RB|=4>|AB|=2,
由椭圆定义得,点R的轨迹方程是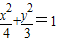 .
.
(2)设M(x,y),则N(-x,-y),QM,QN的斜率分别为kQM,kQN,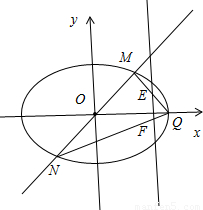
则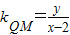 ,
,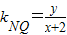 ,
,
∴直线QM的方程为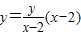 ,直线QN的方程
,直线QN的方程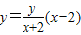 ,
,
令x=t(t≠2),则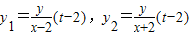 ,
,
又∵(x,y)在椭圆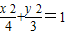 ,∴
,∴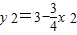 ,
,
∴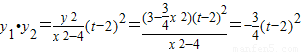 ,其中t为常数.
,其中t为常数.
点评:熟练掌握线段的垂直平分线的性质和椭圆的定义及其性质、直线的斜率计算公式和点斜式等是解题的关键.
(2)设M(x,y),则N(-x,-y),由Q(2,0),可分别表示出QM,QN的斜率,利用点斜式即可得到直线QM,QN的方程,进而即可得到点E,F的纵坐标,再利用点M,N在椭圆上,满足椭圆的方程即可得出.
解答:解:(1)连接RA,由题意得,|RA|=|RP|,|RP|+|RB|=4,
∴|RA|+|RB|=4>|AB|=2,
由椭圆定义得,点R的轨迹方程是
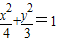 .
.(2)设M(x,y),则N(-x,-y),QM,QN的斜率分别为kQM,kQN,

则
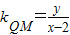 ,
,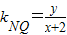 ,
,∴直线QM的方程为
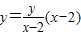 ,直线QN的方程
,直线QN的方程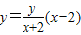 ,
,令x=t(t≠2),则
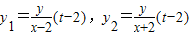 ,
,又∵(x,y)在椭圆
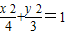 ,∴
,∴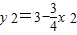 ,
,∴
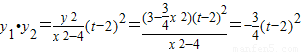 ,其中t为常数.
,其中t为常数.点评:熟练掌握线段的垂直平分线的性质和椭圆的定义及其性质、直线的斜率计算公式和点斜式等是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是