题目内容
1.已知集合A={(x,y)|$\left\{\begin{array}{l}{x≤1}\\{y≤2}\\{x+y≥2}\end{array}\right.$},B={(x,y)|(x+1)2+(y+1)2≤$\frac{4}{5}$},设P(m,n)∈A,Q(s,t)∈B,则$\frac{n-t}{m-s}$的最小值为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
分析 作出区域A和B,$\frac{n-t}{m-s}$表示区域A和B内的点的连线斜率,数形结合由直线和圆相切可得.
解答 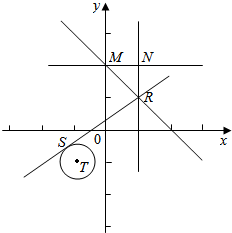 解:作出区域A(如图△MNR及内部)和B(圆T即内部),
解:作出区域A(如图△MNR及内部)和B(圆T即内部),
$\frac{n-t}{m-s}$表示区域A和B内的点的连线斜率,
数形结合可知当直线为图中RS时,直线斜率最小,设斜率为k,
可得直线的点斜式方程为y-1=k(x-1),化为一般式可得kx-y+1-k=0,
由直线和圆相切和点到直线的距离公式可得($\frac{|-k+1+1-k|}{\sqrt{{k}^{2}+1}}$)2=$\frac{4}{5}$,
解方程可得k=$\frac{1}{2}$,或k=2,结合图象可得k=$\frac{1}{2}$,
故选:B.
点评 本题考查简单线性规划,涉及直线和圆的位置关系,准确作图是解决问题的关键,属中档题.

练习册系列答案
相关题目
9.集合A={(x,y)|x-y+4≥0},B={(x,y)|y≥x(x-2)},则集合A∩B的所有元素组成的图形的面积是( )
| A. | $\frac{43}{2}$ | B. | $\frac{55}{2}$ | C. | $\frac{125}{6}$ | D. | 22 |
10.如果点P(sinθ+cosθ,sinθcosθ)位于第二象限,那么角θ所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图所示,E是正方形ABCD所在平面外一点,E在面ABCD上的正投影F恰在AC上,FG∥BC,AB=AE=2,∠EAB=60°.则以下结论中正确的有(1)(2)(4).
如图所示,E是正方形ABCD所在平面外一点,E在面ABCD上的正投影F恰在AC上,FG∥BC,AB=AE=2,∠EAB=60°.则以下结论中正确的有(1)(2)(4).