题目内容
11.在无穷数列{an}中,a1=1,对于任意n∈N*,都有an∈N*,且an<an+1.设集合Am={n|an≤m,m∈N*},将集合Am中的元素的最大值记为bm,即bm是数列{an}中满足不等式an≤m的所有项的项数的最大值,我们称数列{bn}为数列{an}的伴随数列.例如:数列{an}是1,3,4,…,它的伴随数列{bn}是1,1,2,3,….
(Ⅰ)设数列{an}是1,4,5,…,请写出{an}的伴随数列{bn}的前5项;
(Ⅱ)设an=3n-1(n∈N*),求数列{an}的伴随数列{bn}的前20项和;
(Ⅲ)设an=3n-2(n∈N*),求数列{an}的伴随数列{bn}前n项和Sn.
分析 (I)由{an}伴随数列{bn}的定义可得前5项为1,1,1,2,3.
(II)由an=3n-1≤m,可得n≤1+log3m,m∈N*,分类讨论:当1≤m≤2时,m∈N*,b1=b2=1;当3≤m≤8时,m∈N*,b3=b4=…=b8=2;当9≤m≤20时,m∈N*,b9=b10=…=3;即可得出数列{an}的伴随数列{bn}的前20项和;
(III)由an=3n-2≤m,解得n$≤\frac{m+2}{3}$,可得不等式an≤m成立的最大值为bm,因此b1=b2=b3=1,b4=b5=b6=2,…,b3n-2+b3n-1+b3n=t(t∈N*),
分类讨论:当n=3t-2时,当n=3t-1时,当n=3t时,即可得出.
解答 解:(I)由{an}伴随数列{bn}的定义可得前5项为1,1,1,2,3.
(II)由an=3n-1≤m,可得n≤1+log3m,m∈N*,
∴当1≤m≤2时,m∈N*,b1=b2=1;
当3≤m≤8时,m∈N*,b3=b4=…=b8=2;
当9≤m≤20时,m∈N*,b9=b10=…=3;
∴数列{an}的伴随数列{bn}的前20项和=1×2+2×6+3×12=50;
(III)由an=3n-2≤m,解得n$≤\frac{m+2}{3}$,
∵不等式an≤m成立的最大值为bm,
∴b1=b2=b3=1,b4=b5=b6=2,…,b3n-2+b3n-1+b3n=t(t∈N*),
∴当n=3t-2时,(t∈N*),Sn=$3×\frac{1+(t-1)}{2}$(t-1)+t=$\frac{3{t}^{2}-t}{2}$=$\frac{1}{6}(n+1)(n+2)$;
当n=3t-1时,(t∈N*),Sn=$3×\frac{1+(t-1)}{2}(t-1)+2t$=$\frac{3{t}^{2}+t}{2}$=$\frac{1}{6}(n+1)(n+2)$;
当n=3t时,(t∈N*),Sn=$3×\frac{1+t}{2}×t$=$\frac{3({t}^{2}+t)}{2}$=$\frac{1}{6}n(n+3)$.
∴Sn=$\left\{\begin{array}{l}{\frac{(n+1)(n+2)}{6},(n=3t-2或3t-1)}\\{\frac{n(n+3)}{6},(n=3t)}\end{array}\right.$(t∈N*).
点评 本题考查了新定义“伴随数列”、等差数列的通项公式及其前n项和公式,考查了分析问题与解决问题的能力,考查了推理能力与计算能力,属于难题.

| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
| A. | $\frac{{9-4\sqrt{2}}}{7}$ | B. | $\frac{{2-\sqrt{2}}}{7}$ | C. | $\frac{{9+4\sqrt{2}}}{7}$ | D. | $\frac{{2+\sqrt{2}}}{7}$ |
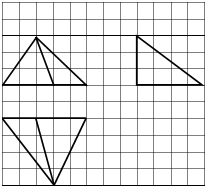 如图,网格纸上小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为( )
如图,网格纸上小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |