题目内容
(本小题满分12分)设函数f(x)的定义域是R,对于任意实数m,n,恒有f(m+n)=f(m)f(n),且当x>0时,0<f(x)<1。
(1)求证:f(0)=1,且当x<0时,有f(x)>1;
(2)判断f(x)在R上的单调性;
⑶设集合A={(x,y)|f(x2)f(y2)>f(1)},集合B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B=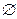 ,求a的取值范围。
,求a的取值范围。
(1)求证:f(0)=1,且当x<0时,有f(x)>1;
(2)判断f(x)在R上的单调性;
⑶设集合A={(x,y)|f(x2)f(y2)>f(1)},集合B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B=
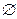 ,求a的取值范围。
,求a的取值范围。解:⑴f(m+n)=f(m)f(n),令m=1,n=0,则f(1)=f(1)f(0),且由x>0时,0<f(x)<1,∴f(0)=1;设m=x<0,n=-x>0,∴f(0)=f(x)f(-x),∴f(x)=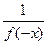 >1。……………4分
>1。……………4分
⑵设x1<x2,则x2-x1>0,∴0<f(x2-x1)<1,∴f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)f(x1)-f(x1)=f(x1)[f(x2-x1)-1]<0,∴f(x)在R上单调递减。……………8分
⑶∵f(x2)f(y2)>f(1),∴f(x2+y2)>f(1),由f(x)单调性知x2+y2<1,又f(ax-y+2)=1=f(0),
∴ax-y+2=0,又A∩B=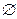 ,∴
,∴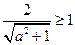 ,∴a2+1≤4,从而
,∴a2+1≤4,从而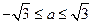 。……12分
。……12分
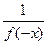 >1。……………4分
>1。……………4分⑵设x1<x2,则x2-x1>0,∴0<f(x2-x1)<1,∴f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)f(x1)-f(x1)=f(x1)[f(x2-x1)-1]<0,∴f(x)在R上单调递减。……………8分
⑶∵f(x2)f(y2)>f(1),∴f(x2+y2)>f(1),由f(x)单调性知x2+y2<1,又f(ax-y+2)=1=f(0),
∴ax-y+2=0,又A∩B=
 ,∴
,∴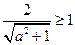 ,∴a2+1≤4,从而
,∴a2+1≤4,从而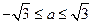 。……12分
。……12分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
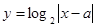 图象的对称轴为
图象的对称轴为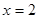 ,则
,则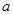 的值为( )
的值为( )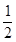
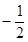
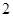
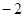
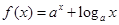
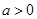 且
且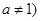 在
在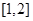 上的最大值与最小值之和为
上的最大值与最小值之和为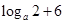 ,则
,则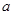 的值为 ( )
的值为 ( )



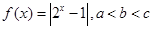 ,且
,且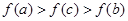 ,则下列结论中,必成立的是( )
,则下列结论中,必成立的是( )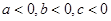

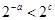
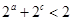
 ,则f(
,则f( )等于( )
)等于( )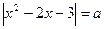 有两个实数根,则
有两个实数根,则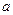 的取值范围是
的取值范围是  ,
, ,
, ,则
,则 三者的大小关系是( )
三者的大小关系是( )


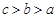
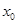 是方程式
是方程式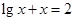 的解,则
的解,则 的定义域是( )
的定义域是( )


