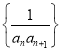题目内容
【题目】设函数![]() .
.
(1)若![]() ,求函数在
,求函数在![]() 的切线方程;
的切线方程;
(2)若函数![]() 在
在![]() 上为单调递减函数,求实数
上为单调递减函数,求实数![]() 的最小值;
的最小值;
(3)若存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析: (1)若![]() ,写出函数
,写出函数![]() ,求出切点和斜率,即可写出切线方程;(2) 函数可化为
,求出切点和斜率,即可写出切线方程;(2) 函数可化为![]() ,
,![]() 在
在![]() 上为单调递减函数,即导函数小于等于0在在
上为单调递减函数,即导函数小于等于0在在![]() 上恒成立,分离参变量,转化为构造出的新函数最值问题,对新函数求导,判断单调性求出最值即可;(3) 存在
上恒成立,分离参变量,转化为构造出的新函数最值问题,对新函数求导,判断单调性求出最值即可;(3) 存在![]() ,使得
,使得![]() 成立,即
成立,即![]() ,又
,又![]() ,即f(x)min
,即f(x)min![]()
![]() ,根据
,根据![]() 的导函数对参数进行讨论,分别得出单调性进而求出最小值,代入不等式求出a的范围.
的导函数对参数进行讨论,分别得出单调性进而求出最小值,代入不等式求出a的范围.
试题解析:(1)若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以所求切线为![]()
(2)函数可化为![]() ,
,![]() 在
在![]() 上为单调递减函数,
上为单调递减函数,![]() 在
在![]() 上恒成立,
上恒成立,![]() 恒成立,令
恒成立,令![]() ,则
,则![]() ,
,
可知![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,所在
单调递减,所在![]() ,
,![]()
最小值是![]()
(3)命题等价于“当![]() 时,有f(x)min
时,有f(x)min![]() f′(x)max+a”,
f′(x)max+a”,
由(Ⅰ)知,当x∈[e,e2]时,lnx∈[1,2],![]() ,
,
![]() =
=![]() ,
,
![]()
问题等价于:“当x∈[e,e2]时,有f(x)min![]()
![]() ”,
”,
①a![]()
![]() 时,由(2),f(x)在[e,e2]上为减函数,
时,由(2),f(x)在[e,e2]上为减函数,
则f(x)min=f(e2)=![]()
∴![]() .
.
![]()
②当![]()
由于![]() 在
在![]() 上为增函数,所以
上为增函数,所以![]() 的值域为
的值域为![]()
即![]()
若![]() ,即
,即![]() ,
,![]() 恒成立,所以
恒成立,所以![]() 为增函数,于是
为增函数,于是
![]() ,不合题意
,不合题意
若![]() ,
,![]() ,由
,由![]() 的单调性和值域知
的单调性和值域知
存在唯一![]() ,使得
,使得![]() ,且
,且
![]() ,
,![]() ,
,![]() 为减函数
为减函数
![]() ,
,![]() ,
,![]() 为增函数
为增函数
![]()
所以![]()
与![]() 矛盾
矛盾
综上,实数a的取值范围为![]() .
.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某城市为鼓励人们绿色出行,乘坐地铁,地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策,不超过![]() 站的地铁票价如下表:
站的地铁票价如下表:
乘坐站数 |
|
|
|
票价(元) |
|
|
|
现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过![]() 站.甲、乙乘坐不超过
站.甲、乙乘坐不超过![]() 站的概率分别为
站的概率分别为![]() ,
, ![]() ;甲、乙乘坐超过
;甲、乙乘坐超过![]() 站的概率分别为
站的概率分别为![]() ,
, ![]() .
.
(1)求甲、乙两人付费相同的概率;
(2)设甲、乙两人所付费用之和为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】某快餐代卖店代售多种类型的快餐,深受广大消费者喜爱.其中,![]() 种类型的快餐每份进价为
种类型的快餐每份进价为![]() 元,并以每份
元,并以每份![]() 元的价格销售.如果当天20:00之前卖不完,剩余的该种快餐每份以
元的价格销售.如果当天20:00之前卖不完,剩余的该种快餐每份以![]() 元的价格作特价处理,且全部售完.
元的价格作特价处理,且全部售完.
(1)若该代卖店每天定制![]() 份
份![]() 种类型快餐,求
种类型快餐,求![]() 种类型快餐当天的利润
种类型快餐当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:份,
(单位:份,![]() )的函数解析式;
)的函数解析式;
(2)该代卖店记录了一个月![]() 天的
天的![]() 种类型快餐日需求量(每天20:00之前销售数量)
种类型快餐日需求量(每天20:00之前销售数量)
日需求量 |
|
|
|
|
|
|
天数 |
|
|
|
|
|
|
(i)假设代卖店在这一个月内每天定制![]() 份
份![]() 种类型快餐,求这一个月
种类型快餐,求这一个月![]() 种类型快餐的日利润(单位:元)的平均数(精确到
种类型快餐的日利润(单位:元)的平均数(精确到![]() );
);
(ii)若代卖店每天定制![]() 份
份![]() 种类型快餐,以
种类型快餐,以![]() 天记录的日需求量的频率作为日需求量发生的概率,求
天记录的日需求量的频率作为日需求量发生的概率,求![]() 种类型快餐当天的利润不少于
种类型快餐当天的利润不少于![]() 元的概率.
元的概率.