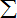题目内容
若(2x+
)6=a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6，则(a0+a2+a4+a6)2-(a1+a3+a5)2的值为______．
| 3 |
∵(2x+
)6=a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6，
令x=1，则有（2+
）6=a0+a1+a2+a3+a4+a5+a6，
令x=-1，则有（-2+
）6=a0-a1+a2-a3+a4-a5+a6，
∴（a0+a2+a4+a6）2-（a1+a3+a5）2=（a0+a1+a2+a3+a4+a5+a6）（a0-a1+a2-a3+a4-a5+a6）=（2+
）6（-2+
）6=[（2+
）（-2+
）]6=（-1）6=1，
∴（a0+a2+a4+a6）2-（a1+a3+a5）2=1．
故答案为：1．
| 3 |
令x=1，则有（2+
| 3 |
令x=-1，则有（-2+
| 3 |
∴（a0+a2+a4+a6）2-（a1+a3+a5）2=（a0+a1+a2+a3+a4+a5+a6）（a0-a1+a2-a3+a4-a5+a6）=（2+
| 3 |
| 3 |
| 3 |
| 3 |
∴（a0+a2+a4+a6）2-（a1+a3+a5）2=1．
故答案为：1．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
