题目内容
【题目】已知函数f(x)=|2x﹣1|﹣a.
(1)当a=1时,解不等式f(x)>x+1;
(2)若存在实数x,使得f(x)![]() f(x+1),求实数a的取值范围.
f(x+1),求实数a的取值范围.
【答案】(1){x|x>3或x![]() }.(2)(﹣2,+∞).
}.(2)(﹣2,+∞).
【解析】
(1)分![]() 与
与![]() 两种情况求解
两种情况求解![]() 即可.
即可.
(2)代入![]() 到不等式
到不等式![]() 中,再根据能成立问题,分
中,再根据能成立问题,分![]() 的不同取值去绝对值,参变分离求函数最值即可.
的不同取值去绝对值,参变分离求函数最值即可.
解(1)当a=1时,由f(x)>x,得|2x﹣1|﹣1>x+1.
当x![]() 时,2x﹣1﹣1>x+1,解得x>3.
时,2x﹣1﹣1>x+1,解得x>3.
当x![]() 时,1﹣2x﹣1>x+1,解得x
时,1﹣2x﹣1>x+1,解得x![]() .综上可知,不等式f(x)>x+1的解集为 {x|x>3或x
.综上可知,不等式f(x)>x+1的解集为 {x|x>3或x![]() }.
}.
(2)因为![]() ,得
,得![]() .即
.即![]() .
.
令![]() ,
,
则存在实数![]() ,使得
,使得![]() 成立等价于
成立等价于![]() .
.
因为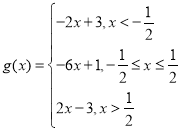 ,故当
,故当![]() 时,
时, ![]()
故![]() .即实数
.即实数![]() 的取值范围为
的取值范围为![]()

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目

