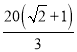题目内容
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)若![]() 的定义域为
的定义域为![]() ,判断
,判断![]() 的单调性,并加以说明;
的单调性,并加以说明;
(2)当![]() 时,是否存在
时,是否存在![]() ,
,![]() ,使得
,使得![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,若存在,求
,若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)当![]() 时,
时,![]() 为减函数,当
为减函数,当![]() 时,
时,![]() 为增函数.证明见解析;(2)存在,
为增函数.证明见解析;(2)存在,![]()
【解析】
(1)求出函数定义域,利用定义法证明![]() 函数单调性,再分类讨论得函数单调性;
函数单调性,再分类讨论得函数单调性;
(2)根据定义域和值域,结合(1)所得单调性,将问题转化为方程![]() 有两个大于3的不同的实数根,利用根的分布求解.
有两个大于3的不同的实数根,利用根的分布求解.
(1)![]() 或
或![]() .由于
.由于![]() 的定义域为
的定义域为![]() ,则
,则![]() .
.
设![]() ,有
,有![]() ,
,
故当![]() 时,
时,![]() 为减函数,当
为减函数,当![]() 时,
时,![]() 为增函数.
为增函数.
(2)若![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
由(1)知当![]() 时,
时,![]() 为减函数.
为减函数.
则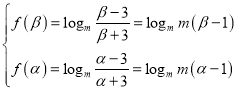 ,
,
即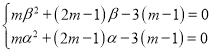 ,又
,又![]() ,
,
即![]() ,
,![]() 为方程
为方程![]() 的大于3的两个不同的实数根.
的大于3的两个不同的实数根.
从而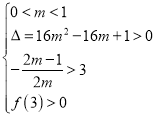 得
得![]() .
.
故当![]() 时,存在满足题意条件的
时,存在满足题意条件的![]() ,
,![]() .
.

练习册系列答案
相关题目
【题目】已知某单位甲、乙、丙三个部门共有员工60人,为调查他们的睡眠情况,逦过分层抽样获得12名员工每天睡眠的时间,数据如下表(单位:小时)
甲部门 | 6 | 7 | 8 | ||
乙部门 | 6 | 6.5 | 7 | 7.5 | |
丙部门 | 5.5 | 6 | 6.5 | 7 | 8.5 |
(1)求该单位乙部门的员工人数;
(2)若将每天睡眠时间不少于7小时视为睡眠充足,现从该单位任抽取1人,估计抽到的此人为睡眠充足者的概率;
(3)从甲部门和乙部门抽出的员工中,各随机选取一人,甲部门选出的员工记为A,乙部门选出的员工记为B.假设所有员工睡眠的时间相互独立.求A的睡眠时间不少于B的睡眠时间的概率.