题目内容
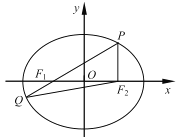
【题目】已知抛物线![]() ,过点
,过点![]() 的动直线
的动直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点
两点
(1)当![]() 恰为
恰为![]() 的中点时,求直线
的中点时,求直线![]() 的方程;
的方程;
(2)抛物线上是否存在一个定点![]() ,使得以弦
,使得以弦![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)利用点差可求![]() ,从而得到直线
,从而得到直线![]() 的方程.
的方程.
(2)设![]() ,设
,设![]() ,
,![]() ,
,![]() ,联立直线方程和抛物线方程后消元可得
,联立直线方程和抛物线方程后消元可得![]() ,利用
,利用![]() 及韦达定理可以得到
及韦达定理可以得到![]() 恒成立,故求得
恒成立,故求得![]() .
.
(1)设![]() ,
,![]() 两点坐标分别为
两点坐标分别为![]() ,
,![]() ,当
,当![]() 恰为
恰为![]() 的中点时,
的中点时,
显然![]() ,故
,故![]() ,又
,又![]() ,故
,故![]()
则直线![]() 的方程为
的方程为![]()
(2)假设存在定点![]() ,设
,设![]() ,当直线
,当直线![]() 斜率存在时,设
斜率存在时,设![]() ,
,![]() ,
,![]() ,联立
,联立![]()
整理得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由以弦![]() 为直径的圆恒过点
为直径的圆恒过点![]() 知
知![]() ,
,
即![]()
即![]()
![]()
故![]() ,即
,即![]()
整理得![]()
即当![]() 时,恒有
时,恒有![]() ,故存在定点
,故存在定点![]() 满足题意;
满足题意;
当直线![]() 斜率不存在时,
斜率不存在时,![]() ,不妨令
,不妨令![]() ,
,![]() ,
,![]() ,也满足
,也满足![]()
综上所述,存在定点![]() ,使得以弦
,使得以弦![]() 为直径的圆恒过点
为直径的圆恒过点![]()

 特高级教师点拨系列答案
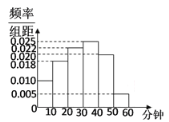
特高级教师点拨系列答案【题目】某电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于40分钟的观众称为体育迷.若抽取100人中有女性55人,其中女体育迷有10人,完成答题卡中的列联表并判断能否在犯错误概率不超过0.05的前提下认为体育迷与性别有关系?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
附表及公式: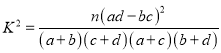 ,
,![]() .
.
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
【题目】足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校y(百个) | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱.
(已知:![]() ,则认为y与x线性相关性很强;
,则认为y与x线性相关性很强;![]() ,则认为y与x线性相关性一般;
,则认为y与x线性相关性一般;![]() ,则认为y与x线性相关性较):
,则认为y与x线性相关性较):
(2)求y关于x的线性回归方程,并预测A地区2020年足球特色学校的个数(精确到个).
参考公式和数据: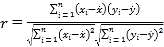 ,
,
![]()
![]()
![]() ,
,
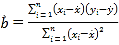
![]() .
.
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如表的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
算得,![]() .见附表:参照附表,得到的正确结论是( )
.见附表:参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C. 有99%以上的把握认为“爱好该项运动与性别有关”
D. 有99%以上的把握认为“爱好该项运动与性别无关”