题目内容
【题目】若数列{an}满足:对任意n∈N*,均有an=bn+cn成立,且{bn},{cn}都是等比数列,则称(bn,cn)是数列{an}的一个等比拆分.
(1)若an=2n,且(bn,bn+1)是数列{an}的一个等比拆分,求{bn}的通项公式;
(2)设(bn,cn)是数列{an}的一个等比拆分,且记{bn},{cn}的公比分别为q1,q2;
①若{an}是公比为q的等比数列,求证:q1=q2=q;
②若a1=1,a2=2,q1q2=﹣1,且对任意n∈N*,an+13<anan+1an+2+an+2﹣an恒成立,求a3的取值范围.
【答案】(1)![]() .(2)①答案见解析, ②(3,7).
.(2)①答案见解析, ②(3,7).
【解析】
(1)设数列{bn}的公比为q0,根据已知求出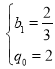 ,即得{bn}的通项公式;(2)①由an=bn+cn,可得
,即得{bn}的通项公式;(2)①由an=bn+cn,可得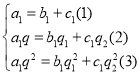 , 令n=1,2,3得:
, 令n=1,2,3得: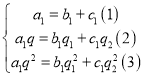 ,对方程进行分析得q1=q2=q; ②令Tn
,对方程进行分析得q1=q2=q; ②令Tn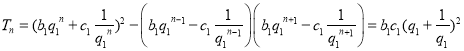 ,证明对任意n∈N*,均有Tn+1=﹣Tn成立,得
,证明对任意n∈N*,均有Tn+1=﹣Tn成立,得![]() ,可得
,可得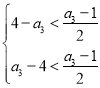 ,解得3<a3<7.
,解得3<a3<7.
(1)设数列{bn}的公比为q0,则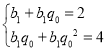 (b1q0≠0)对任意n∈N*成立,
(b1q0≠0)对任意n∈N*成立,
令n=1,2可得: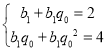 ,解得:
,解得: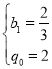 ,
,
∴![]() ,经检验符合题意;
,经检验符合题意;
(2)①由an=bn+cn,可得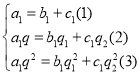 ,
,
令n=1,2,3得: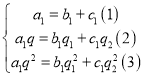
(1)代入(2)得b1(q1﹣q)=c1(q﹣q2), (2)代入(3)得b1q1(q1﹣q)=c1q2(q﹣q2),
如果q1,q2不全等于q,显然它们一定都不等于q,
因此考虑q1≠q且q2≠q的情况,此时用后式除以前式可得q1=q2,
再将其代入到a1=b1+c1,a1q=b1q1+c1q2,可得q1=q2=q,矛盾,
因此只能q1=q2=q,经验证符合题意;
②令Tn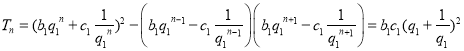 ,
,
则当n为偶数时,![]() ,
,
同理,当n为奇数时,可算的![]() ,
,
所以对任意n∈N*,均有Tn+1=﹣Tn成立
由Tn+1=﹣Tn可得![]() ,
,
因为an≠0,因此可化简得![]() ,
,
所以![]() ,
,
要使原不等式恒成立,显然必有an>0,即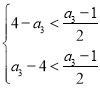 恒成立,
恒成立,
而T1=4﹣a3,因此可得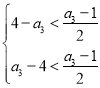 ,解得3<a3<7,
,解得3<a3<7,
综上所述,a3的取值范围为(3,7).

 名校课堂系列答案
名校课堂系列答案