题目内容
已知函数f(x)=  +lnx的图像在点P(m,f(m))处的切线方程为y="x" ,
+lnx的图像在点P(m,f(m))处的切线方程为y="x" ,
设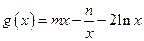 .
.
(1)求证:当 恒成立;
恒成立;
(2)试讨论关于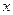 的方程:
的方程: 根的个数.
根的个数.
 +lnx的图像在点P(m,f(m))处的切线方程为y="x" ,
+lnx的图像在点P(m,f(m))处的切线方程为y="x" ,设
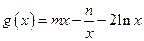 .
. (1)求证:当
 恒成立;
恒成立;(2)试讨论关于
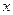 的方程:
的方程: 根的个数.
根的个数. (1)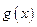
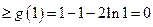 对于
对于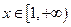 恒成立.
恒成立.
(2)①当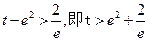 时,方程无解.
时,方程无解.
②当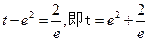 时,方程有一个根.
时,方程有一个根.
③当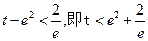 时,方程有两个根.
时,方程有两个根.
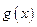
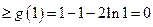 对于
对于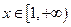 恒成立.
恒成立. (2)①当
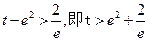 时,方程无解.
时,方程无解. ②当
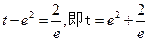 时,方程有一个根.
时,方程有一个根.③当
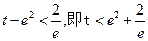 时,方程有两个根.
时,方程有两个根.1)由k=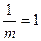 得m=1
得m=1 ∴f(m)=1=n+0,n=1
∴f(m)=1=n+0,n=1
∴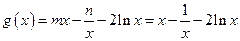 .
.
∴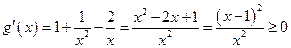 ,
,
∴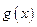 在
在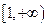 是单调增函数,
是单调增函数,
∴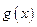
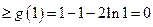 对于
对于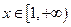 恒成立.
恒成立.
(2)方程 ,∴
,∴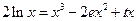 .
.
∵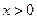 ,∴ 方程为
,∴ 方程为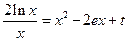 .
.
令 ,
,
 ,当
,当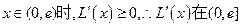 上为增函数;
上为增函数;
 上为减函数,
上为减函数,
当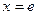 时,
时,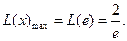
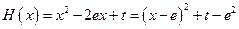 ,
,
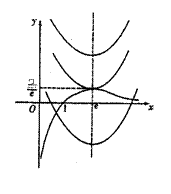
∴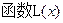 、
、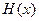 在同一坐标系的大致图象如图所示,
在同一坐标系的大致图象如图所示,
∴①当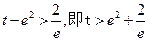 时,方程无解.
时,方程无解.
②当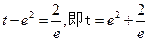 时,方程有一个根.
时,方程有一个根.
③当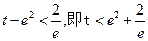 时,方程有两个根.
时,方程有两个根.
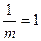 得m=1
得m=1 ∴f(m)=1=n+0,n=1
∴f(m)=1=n+0,n=1
∴
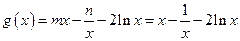 .
.∴
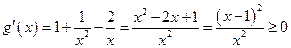 ,
,∴
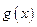 在
在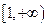 是单调增函数,
是单调增函数,∴
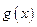
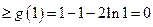 对于
对于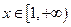 恒成立.
恒成立.(2)方程
 ,∴
,∴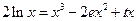 .
.∵
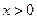 ,∴ 方程为
,∴ 方程为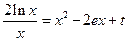 .
.令
 ,
, ,当
,当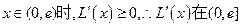 上为增函数;
上为增函数; 上为减函数,
上为减函数,当
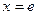 时,
时,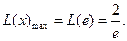
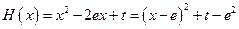 ,
,∴
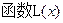 、
、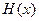 在同一坐标系的大致图象如图所示,
在同一坐标系的大致图象如图所示,∴①当
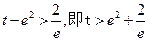 时,方程无解.
时,方程无解. ②当
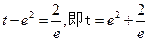 时,方程有一个根.
时,方程有一个根.③当
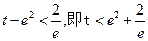 时,方程有两个根.
时,方程有两个根.
练习册系列答案
相关题目
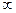 )上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有
)上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有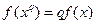 .
.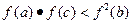 ;
;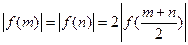 ,求证:
,求证: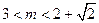
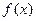 ,若存在闭区间
,若存在闭区间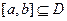 和常数
和常数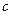 ,使得对任意
,使得对任意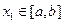 ,都有
,都有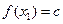 ,且对任意
,且对任意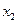 ∈D,当
∈D,当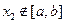 时,
时,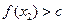 恒成立,则称函数
恒成立,则称函数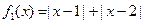 和
和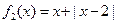 是否为R上的“平底型”函数? 并说明理由;
是否为R上的“平底型”函数? 并说明理由;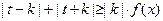 对一切
对一切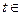 R恒成立,求实数
R恒成立,求实数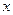 的取值范围;
的取值范围;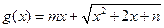 是区间
是区间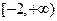 上的“平底型”函数,求
上的“平底型”函数,求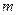 和
和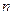 的值.
的值.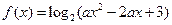
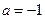 时,求该函数的定义域和值域;
时,求该函数的定义域和值域;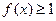 在区间
在区间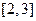 上恒成立,求实数
上恒成立,求实数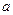 的取值范围.
的取值范围.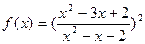 (其中
(其中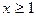 且
且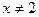 )
)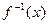
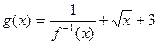 ,求函数g(x)最小值及相应的x值;
,求函数g(x)最小值及相应的x值;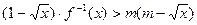 对于区间
对于区间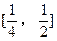 上的每一个x值都成立,求实数m的取值范围。
上的每一个x值都成立,求实数m的取值范围。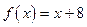 ,
,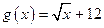 ,及任意的
,及任意的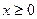 ,当甲公司投入
,当甲公司投入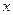 万元作宣传时,乙公司投入的宣传费若小于
万元作宣传时,乙公司投入的宣传费若小于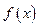 万元,则乙公司有失败的危险,否则无失败的危险;当乙公司投入
万元,则乙公司有失败的危险,否则无失败的危险;当乙公司投入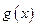 万元,则甲公司有失败的危险,否则无失败的危险. 设甲公司投入宣传费x万元,乙公司投入宣传费y万元,建立如图直角坐标系,试回答以下问题:
万元,则甲公司有失败的危险,否则无失败的危险. 设甲公司投入宣传费x万元,乙公司投入宣传费y万元,建立如图直角坐标系,试回答以下问题: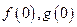 ;
;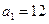 万元,乙在上述策略下,投入最少费用
万元,乙在上述策略下,投入最少费用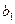 ;而甲根据乙的情况,调整宣传费为
;而甲根据乙的情况,调整宣传费为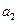 ;同样,乙再根据甲的情况,调整宣传费为
;同样,乙再根据甲的情况,调整宣传费为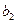
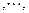 如此得当甲调整宣传费为
如此得当甲调整宣传费为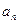 时,乙调整宣传费为
时,乙调整宣传费为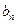 ;试问是否存在
;试问是否存在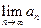 ,
,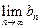 的值,若存在写出此极限值(不必证明),若不存在,说明理由.
的值,若存在写出此极限值(不必证明),若不存在,说明理由. 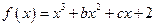 在
在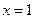 处取得极值
处取得极值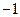 .
.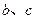 的值;
的值; 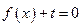 在区间
在区间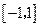 上有实根,求实数的取值范围.
上有实根,求实数的取值范围.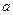 的
的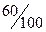 ,目前我国的减排手段有两种,第一种是通过引进新技术,新工艺使得每年的炭排放比上一年炭排放总量均减少
,目前我国的减排手段有两种,第一种是通过引进新技术,新工艺使得每年的炭排放比上一年炭排放总量均减少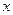 个百分点,第二种是通过教育与宣传使得全体国民具有节能减排的意识,进而减少炭排放。
个百分点,第二种是通过教育与宣传使得全体国民具有节能减排的意识,进而减少炭排放。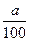 ,求2011年我国的炭排放量
,求2011年我国的炭排放量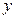 个百分点,要保证完成减排目标,求
个百分点,要保证完成减排目标,求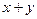 满足的范围。(已知
满足的范围。(已知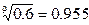 ,
,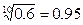 ,
,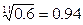 ,
,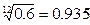 )
)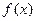 是定义域为
是定义域为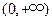 上的增函数,
上的增函数,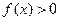 ,且
,且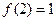 ,指出
,指出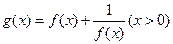 单调区间,并证明你的结论.
单调区间,并证明你的结论.