题目内容
函数 的定义域为D,若存在闭区间[a,b]
的定义域为D,若存在闭区间[a,b] D,使得函数
D,使得函数 满足:
满足:
(1)  在[a,b]内是单调函数;(2)
在[a,b]内是单调函数;(2)  在[a,b]上的值域为[2a,2b],则称区间[a,b]为
在[a,b]上的值域为[2a,2b],则称区间[a,b]为 的“和谐区间”.下列函数中存在“和谐区间”的是 (只需填符合题意的函数序号)
的“和谐区间”.下列函数中存在“和谐区间”的是 (只需填符合题意的函数序号)
① ; ②
; ② ; ③
; ③ ; ④
; ④ .
.
①③④
解析试题分析:函数中存在“和谐区间”,则: 在
在 内时单调函数,且
内时单调函数,且 或
或 ,
,
对于① ,易知函数单调递增,若存在“和谐区间”,则
,易知函数单调递增,若存在“和谐区间”,则 ,所以
,所以 ,
,
所以函数 存在“和谐区间”
存在“和谐区间” .
.
对于② ,易知函数单调递增,若存在“和谐区间”,则
,易知函数单调递增,若存在“和谐区间”,则 ,易知无解.故该函数没有“和谐区间”.
,易知无解.故该函数没有“和谐区间”.
对于③ ,易知函数单调递减,则
,易知函数单调递减,则 ,解得
,解得 ,故有无穷解.存在“和谐区间”.
,故有无穷解.存在“和谐区间”.
④ ,
, ,若存在“和谐区间”,
,若存在“和谐区间”, ,则
,则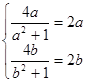 ,
,
所以 ,故存在“和谐区间”. 故填①③④.
,故存在“和谐区间”. 故填①③④.
考点:函数的值域;命题的真假判断与应用.
点评:本题考查新定义,考查学生分析解决问题的能力,涉及知识点较多,需要谨慎计算.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 长度为
长度为 .已知函数
.已知函数 定义域为
定义域为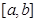 ,值域为
,值域为 ,则区间
,则区间 ,若实数
,若实数 满足
满足 的最小值是____.
的最小值是____. 若
若 ,则
,则 等于 .
等于 .  ,若
,若 ,则
,则 .
. ,若
,若 ,则a= .
,则a= .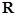 上的偶函数
上的偶函数 ,对任意实数
,对任意实数 都有
都有 ,当
,当 时,
时, ,若在区间
,若在区间 内,函数
内,函数 与函数
与函数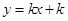 的图象恰有4个交点,则实数
的图象恰有4个交点,则实数 的取值范围是__________.
的取值范围是__________.  满足:①定义域为
满足:①定义域为 ;②对任意
;②对任意 ,有
,有 ;③当
;③当 时,
时, .记
.记 ,根据以上信息,可以得到函数
,根据以上信息,可以得到函数 在区间
在区间 内的零点个数是___ ___.
内的零点个数是___ ___.