题目内容
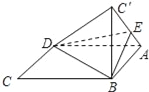
【题目】如图,四面体![]() 中,
中, ![]() 是正三角形,
是正三角形, ![]() 是直角三角形,
是直角三角形, ![]() ,
,![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)过![]() 的平面交
的平面交![]() 于点
于点![]() ,若平面
,若平面![]() 把四面体
把四面体![]() 分成体积相等的两部分,求二面角
分成体积相等的两部分,求二面角![]() 的大小。
的大小。
【答案】(1)证明见解析;(2)![]() 。
。
【解析】
(1)如图所示,取AC的中点O,连接BO,OD.△ABC是等边三角形,可得OB⊥AC.由已知可得:△ABD≌△CBD,AD=CD.△ACD是直角三角形,可得AC是斜边,∠ADC=90°.可得DO=![]() AC.利用DO2+BO2=AB2=BD2.可得OB⊥OD.利用线面面面垂直的判定与性质定理即可证明;
AC.利用DO2+BO2=AB2=BD2.可得OB⊥OD.利用线面面面垂直的判定与性质定理即可证明;
(2)由平面![]() 把四面体
把四面体![]() 分成体积相等的两部分,明确
分成体积相等的两部分,明确![]() 为
为![]() 中点, 易知二面角
中点, 易知二面角![]() 的平面角为
的平面角为![]() .
.
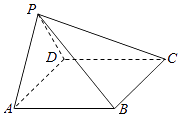
(1)证明:如图所示,取AC的中点O,连接BO,OD.
∵△ABC是等边三角形,∴OB⊥AC.
△ABD与△CBD中,AB=BD=BC,∠ABD=∠CBD,
∴△ABD≌△CBD,∴AD=CD.
∵△ACD是直角三角形,
∴AC是斜边,∴∠ADC=90°.
∴DO=![]() AC.
AC.
∴DO2+BO2=AB2=BD2.
∴∠BOD=90°.
∴OB⊥OD.
又DO∩AC=O,∴OB⊥平面ACD.
又OB平面ABC,
∴平面ACD⊥平面ABC.
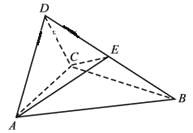
(2)∵平面![]() 把四面体
把四面体![]() 分成体积相等的两部分,
分成体积相等的两部分,
∴![]() ,∴
,∴![]() .
.
∴![]() 即
即![]() 为
为![]() 中点,
中点,
由(1)知![]() 为直角三角形,则
为直角三角形,则![]()
又![]() ,
,
∴![]() 为等边三角形,故
为等边三角形,故![]()
![]() 。
。
由(1)知![]() 则AE=CE,
则AE=CE,
所以![]() ,
,
又![]() ,
,
则二面角![]() 的平面角为
的平面角为![]() ,且二面角的大小为
,且二面角的大小为![]() 。
。

练习册系列答案
相关题目