题目内容
【题目】已知数列{an}满足a1= ![]() ,an+1=10an+1.
,an+1=10an+1.
(1)证明数列{an+ ![]() }是等比数列,并求数列{an}的通项公式;
}是等比数列,并求数列{an}的通项公式;
(2)数列{bn}满足bn=lg(an+ ![]() ),Tn为数列{
),Tn为数列{ ![]() }的前n项和,求证:Tn<
}的前n项和,求证:Tn< ![]() .
.
【答案】
(1)解:由an+1=10an+1得an+1+ ![]() =10an+
=10an+ ![]() =10(an+
=10(an+ ![]() ),
),
∴ 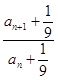 =10,
=10,
∴数列{an+ ![]() }是等比数列,首项为a1+
}是等比数列,首项为a1+ ![]() =100,公比为10,
=100,公比为10,
∴an+ ![]() =100×10n﹣1=10n+1,
=100×10n﹣1=10n+1,
所以an=10n+1﹣ ![]() .
.
(2)解:由(1)可得:bn=lg(an+ ![]() )=lg10n+1=n+1,
)=lg10n+1=n+1,
∴ ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴Tn=( ![]() ﹣
﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )++(
)++( ![]() ﹣
﹣ ![]() )=
)= ![]() ﹣
﹣ ![]() <
< ![]() ,
,
∴Tn< ![]() .
.
【解析】(1)由题意可知:构造等比数列,an+1+ ![]() =10an+
=10an+ ![]() =10(an+
=10(an+ ![]() ),则数列{an+
),则数列{an+ ![]() }是以100为首项,10为公比的等比数列,利用等比数列通项公式,即可求得数列{an}的通项公式;(2)由(1)可知bn=lg(an+
}是以100为首项,10为公比的等比数列,利用等比数列通项公式,即可求得数列{an}的通项公式;(2)由(1)可知bn=lg(an+ ![]() )=n+1,利用“裂项法”即可求得Tn,即可求得Tn<
)=n+1,利用“裂项法”即可求得Tn,即可求得Tn< ![]() .
.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系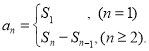 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

【题目】2016世界特色魅力城市200强新鲜出炉,包括黄山市在内的28个中国城市入选.美丽的黄山风景和人文景观迎来众多宾客.现在很多人喜欢自助游,某调查机构为了了解“自助游”是否与性别有关,在黄山旅游节期间,随机抽取了100人,得如下所示的列联表:
赞成“自助游” | 不赞成“自助游” | 合计 | |
男性 | 30 | ||
女性 | 10 | ||
合计 | 100 |
(1)若在100这人中,按性别分层抽取一个容量为20的样本,女性应抽11人,请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料能否在犯错误的概率不超过0.05前提下,认为赞成“自助游”是与性别有关系?
(2)若以抽取样本的频率为概率,从旅游节游客中随机抽取3人赠送精美纪念品,记这3人中赞成“自助游”人数为X,求X的分布列和数学期望. 附:K2= ![]()
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |