题目内容
【题目】体积为 ![]() 的正三棱锥A﹣BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是( )
的正三棱锥A﹣BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是( ) 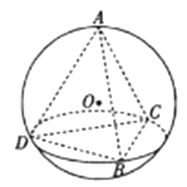
A.[4π,12π]
B.[8π,16π]
C.[8π,12π]
D.[12π,16π]
【答案】B
【解析】解:设BC=3a,则R=2a,
∵体积为 ![]() 的正三棱锥A﹣BCD的每个顶点都在半径为R的球O的球面上,
的正三棱锥A﹣BCD的每个顶点都在半径为R的球O的球面上,
∴ ![]() =
= ![]() ,∴h=
,∴h= ![]() ,
,
∵R2=(h﹣R)2+( ![]() a)2,∴4a2=(
a)2,∴4a2=( ![]() ﹣2a)2+3a2,∴a=2,
﹣2a)2+3a2,∴a=2,
∴BC=6,R=4,
∵点E为线段BD上一点,且DE=2EB,
∴△ODB中,OD=OB=4,DB=6,cos∠ODB= ![]() ,
,
∴OE= ![]() =2
=2 ![]() ,
,
截面垂直于OE时,截面圆的半径为 ![]() =2
=2 ![]() ,截面圆面积为8π,
,截面圆面积为8π,
以OE所在直线为直径时,截面圆的半径为4,截面圆面积为16π,
∴所得截面圆面积的取值范围是[8π,16π].
故选:B.
【考点精析】本题主要考查了球内接多面体的相关知识点,需要掌握球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长才能正确解答此题.

练习册系列答案
相关题目

