如图所示.设E.F.E1.F1分别是长方体ABCD-A1B1C1D1的棱AB.CD.A1B1.C1D1的中点.则平面EFD1A1与平面BCF1E1的位置关系是( )A．平行B．相交C．异面D．不确定题目和参考答案——青夏教育精英家教网—

题目内容

12．

如图所示，设E，F，E₁，F₁分别是长方体ABCD-A₁B₁C₁D₁的棱AB，CD，A₁B₁，C₁D₁的中点，则平面EFD₁A₁与平面BCF₁E₁的位置关系是（　　）

A．

平行

B．

相交

C．

异面

D．

不确定

分析根据已知条件容易判断E₁B∥A₁E，从而得到E₁B∥平面EFD₁A₁，同样可得到E₁F₁∥平面EFD₁A₁，根据面面平行的判定定理即可得到这两平面平行．

解答解：如图，
根据已知条件知E₁B∥A₁E，A₁E?平面EFD₁A₁，E₁B?平面EFD₁A₁；
∴E₁B∥平面EFD₁A₁；
同理E₁F₁∥平面EFD₁A₁；
又E₁F₁，E₁B?平面BCF₁E₁，且E₁B∩E₁F₁=E₁；
∴平面EFD₁A₁∥平面BCF₁E₁．
故选A．

点评考查平行四边形的定义，以及线面平行的判定定理，面面平行的判定定理．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

16．已知直线l和x轴所成的角为45°，且过点（1，-3），求直线l的方程．

3．在等比数列{a_n}中，n∈N^*，公比0＜q＜1，且a₁+a₄=9，又a₁与a₄的等比中项为2$\sqrt{2}$．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）设b_n=4-log₂a_n，数列{b_n}的前n项和为S_n，求数列{S_n}的通项公式
（Ⅲ）设T_n=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+…+$\frac{1}{{S}_{n}}$，求T_n．

20．数列$\frac{1}{2}$，2$\frac{3}{4}$，4$\frac{7}{8}$，6$\frac{15}{16}$，…的前n项和S_n=n²+（$\frac{1}{2}$）ⁿ-1．

7．在△ABC中，角A，B，C所对的边分别为a，b，c，sin²A+sin²B+sin²C=2$\sqrt{3}$sinAsinBsinC，且a=2，则△ABC的外接圆半径R=$\frac{2\sqrt{3}}{3}$．

17．根据如图样本数据得到的回归方程为$\widehat{y}$=bx+a，若样本点的中心为（5，0.9）．则当x每增加1个单位时，y就（　　）

x	3	4	5	6	7
y	4.0	a-5.4	-0.5	0.5	b-0.6

4．若x，y为实数，且$\sqrt{{x}^{2}+{y}^{2}}$+yi=4+2i，求x，y．

1．

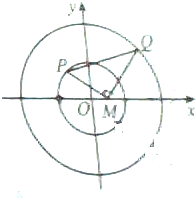如图，已知圆E₁：x²+y²=4，E₂：x²+y²=16，点M（1，0），动点P，Q分别在圆E₁，E₂上，且MP⊥MQ．
（1）在x轴上是否存在点N，使得|PN|=2|PM|？若存在，求出点N的坐标；否则，说明理由；
（2）求|PQ|的取值范围．

2．若在△ABC中，2cosBsinA=sinC，则△ABC的形状一定是（　　）

试题分类