题目内容
(本小题满分14分)
设函数 ,试求函数f(x)存在最小值的充要条件,并求出相应的最小值.
,试求函数f(x)存在最小值的充要条件,并求出相应的最小值.
设函数
 ,试求函数f(x)存在最小值的充要条件,并求出相应的最小值.
,试求函数f(x)存在最小值的充要条件,并求出相应的最小值.– a2
由条件得:f (x )=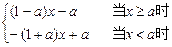 , 4分
, 4分
∵a > 0,
∴ – (1 + a )< 0, f (x )在(–∞,a)上是减函数.
如果函数f (x )存在最小值,则f (x )在[a,+ ∞)上是增函数或常数.
∴1 – a ³ 0,
得a £ 1,
又a > 0, ∴0< a £ 1. 5分
反之,当0< a £ 1时,
(1 – a ) ³ 0, ∴f (x )在f[a,+ ∞)上是增函数或常数.
–(1 + a )< 0, ∴f (x )在(–∞,a)上是减函数.
∴f(x )存在最小值f(a).
综合上述f (x )存在最小值的充要条件是0< a £ 1,此时f (x)min =" –" a2 3分
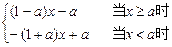 , 4分
, 4分∵a > 0,
∴ – (1 + a )< 0, f (x )在(–∞,a)上是减函数.
如果函数f (x )存在最小值,则f (x )在[a,+ ∞)上是增函数或常数.
∴1 – a ³ 0,
得a £ 1,
又a > 0, ∴0< a £ 1. 5分
反之,当0< a £ 1时,
(1 – a ) ³ 0, ∴f (x )在f[a,+ ∞)上是增函数或常数.
–(1 + a )< 0, ∴f (x )在(–∞,a)上是减函数.
∴f(x )存在最小值f(a).
综合上述f (x )存在最小值的充要条件是0< a £ 1,此时f (x)min =" –" a2 3分

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
 ,则
,则 (10)值为( )
(10)值为( )
 .
. ,求函数
,求函数 在区间
在区间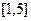 的值域;
的值域; 上为增函数,求
上为增函数,求 的取值范围.
的取值范围.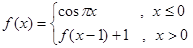 ,则
,则 的值为
的值为

 上的奇函数和偶函数,当x <0时,
上的奇函数和偶函数,当x <0时, ,且g(-3)=0,则不等式f(x)g(x)<0的解集是 ( )
,且g(-3)=0,则不等式f(x)g(x)<0的解集是 ( )



 ,若
,若 且
且 .
. .
.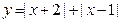 的最小值为
的最小值为  则
则 ( )
( )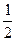

 (xÎR),给出下列命题:
(xÎR),给出下列命题: 上是增函数;
上是增函数; ,
,