��Ŀ����
����˵����
�ٺ���y=log
(x2-2x-3)�ĵ����������ǣ�-�ޣ�1����
��������y=f��x��������ΪR������f��1-x��=f��x+1����������ͼ�����y��Գƣ�
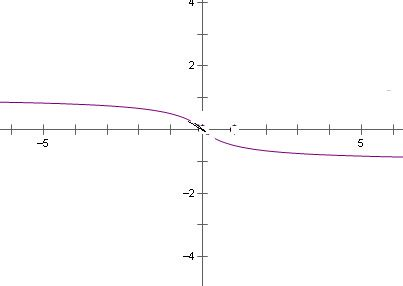
�ۺ���f��x��=
��x��R����ֵ��Ϊ��-1��1����
�ܺ���y=|3-x2|��ͼ���ֱ��y=a��a��R���Ĺ����������m����m��ֵ������0��2��3��4��
��������f��x��=x2-2ax+5��a��1����x��[1��3]������㣬��ʵ��a��ȡֵ��Χ��[
��3]��
������ȷ�������
�ٺ���y=log
| 1 |
| 2 |
��������y=f��x��������ΪR������f��1-x��=f��x+1����������ͼ�����y��Գƣ�
�ۺ���f��x��=
| x |
| 1+|x| |
�ܺ���y=|3-x2|��ͼ���ֱ��y=a��a��R���Ĺ����������m����m��ֵ������0��2��3��4��
��������f��x��=x2-2ax+5��a��1����x��[1��3]������㣬��ʵ��a��ȡֵ��Χ��[
| 5 |
������ȷ�������
�ۢܢ�
�ۢܢ�
�����������ݵ�x=0ʱ�������Ľ���ʽ��������жϢ٣����ݺ����Գ��ԣ��ɵú���y=f��x����ͼ�����ֱ��x=1�Գƣ����жϢڣ���������f��x��=
��x��R����ͼ��Ϻ���ͼ�������������ֵ���жϢۣ���������y=|3-x2|��ͼ�ɷ���������y=|3-x2|��ͼ���ֱ��y=a��a��R���Ĺ�������������жϢܣ����ݶ��κ�����ͼ������ʷ���������f��x��=x2-2ax+5��a��1����x��[1��3]������㣬ʵ��a��ȡֵ��Χ�����жϢݣ�
| x |
| 1+|x| |
��� �⣺��x=0ʱ��x2-2x-3=-3����ʱlog
�⣺��x=0ʱ��x2-2x-3=-3����ʱlog
(x2-2x-3)�����壬�ʢٴ���
������y=f��x������f��1-x��=f��x+1��������y=f��x����ͼ�����ֱ��x=1�Գƣ��ʢڴ���
��������f��x��=
��x��R����ͼ����ͼ����ͼ�ɵú�����ֵ��Ϊ��-1��1����
��������y=|3-x2|��ͼ����ͼ��֪������y=|3-x2|��ͼ���ֱ��y=a�����������0��2��3��4�����ʢ���ȷ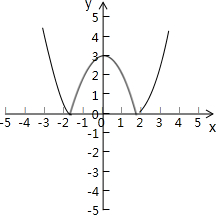
��f��x����x��[1��3]������㣬��f��x��=0��x��[1��3]����ʵ����
��2a=x+
��x��[1��3]����ʵ����
��g��x��=x+
��g��x����[1��
]�����ݼ����ڣ�
��3]����������g��1��=6��g��3��=
����2
��g��x����6����2
��2a��6����
��a��3�ʢ���ȷ
�ʴ�Ϊ���ۢܢ�
 �⣺��x=0ʱ��x2-2x-3=-3����ʱlog
�⣺��x=0ʱ��x2-2x-3=-3����ʱlog| 1 |
| 2 |
������y=f��x������f��1-x��=f��x+1��������y=f��x����ͼ�����ֱ��x=1�Գƣ��ʢڴ���
��������f��x��=
| x |
| 1+|x| |
��������y=|3-x2|��ͼ����ͼ��֪������y=|3-x2|��ͼ���ֱ��y=a�����������0��2��3��4�����ʢ���ȷ
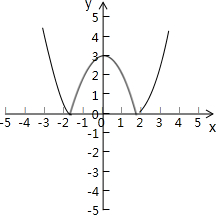
��f��x����x��[1��3]������㣬��f��x��=0��x��[1��3]����ʵ����
��2a=x+
| 5 |
| x |
��g��x��=x+
| 5 |
| x |
| 5 |
| 5 |
| 14 |
| 3 |
| 5 |
| 5 |
| 5 |
�ʴ�Ϊ���ۢܢ�
���������⿼���֪ʶ���Ǹ��Ϻ����ĵ����ԣ������ĶԳ��ԣ�������ֵ����ͼ��Ľ��㣬��������㣬�Ǻ������ݵ��ۺ�Ӧ�ã��Ѷ��е���

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ