题目内容
下列说法:
①函数y=log
(x2-2x-3)的单调增区间是(-∞,1);
②若函数y=f(x)定义域为R且满足f(1-x)=f(x+1),则它的图象关于y轴对称;
③对于指数函数y=2x与幂函数y=x2,总存在x0,当x>x0时,有2x>x2成立;
④若关于x的方程|x|(x+2)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,则x1+x2+x3的取值范围是(-2,
-3).
其中正确的说法是
①函数y=log
| 1 |
| 2 |
②若函数y=f(x)定义域为R且满足f(1-x)=f(x+1),则它的图象关于y轴对称;
③对于指数函数y=2x与幂函数y=x2,总存在x0,当x>x0时,有2x>x2成立;
④若关于x的方程|x|(x+2)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,则x1+x2+x3的取值范围是(-2,
| 2 |
其中正确的说法是
③④
③④
.分析:①中,可判断所给增区间不是函数定义域的子集,由此可知①错误;②中,根据所给等式及对称定义可判断②正确;③中,作出两函数图象可知其正确;④中,构造函数y=|x|(x+2),化为分段函数,然后作出图象,利用图象可得结论;
解答: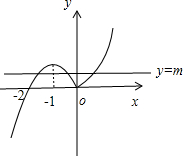
 解:①中,由x2-2x-3>0,得x<-1或x>3,
解:①中,由x2-2x-3>0,得x<-1或x>3,
∴y=log
(x2-2x-3)的定义域为(-∞,-1)∪(3,+∞),
而所给增区间(-∞,1)不是定义域的子集,故①错误;
②中,由f(1-x)=f(1+x),知f(x)的图象关于x=1对称,故②错误;
③中,作出y=2x与y=x2的图象,如图(右一)所示:存在x0=4,当x>4时,有2x>x2成立,故③正确;
④中,构造函数y=|x|(x+2),
(1)当x≥0时,y=x(x+2)=(x+1)2-1;(2)当x<0时,y=-x(x+2)=-(x+1)2+1,对称轴x=-1,
作出图象如图(右二):
∵方程|x|(x+2)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,即两个图象有3个交点,
∴0<m<1,
不妨设 x1<x2<x3,则x1+x2=-2,
当m=1时,x(x+2)=1,得x=-1+
,
此时x3满足0<x3<
-1,
∴x1+x2+x3的取值范围是(-2,
-3),故④正确.
故答案为:③④

 解:①中,由x2-2x-3>0,得x<-1或x>3,
解:①中,由x2-2x-3>0,得x<-1或x>3,∴y=log
| 1 |
| 2 |
而所给增区间(-∞,1)不是定义域的子集,故①错误;
②中,由f(1-x)=f(1+x),知f(x)的图象关于x=1对称,故②错误;
③中,作出y=2x与y=x2的图象,如图(右一)所示:存在x0=4,当x>4时,有2x>x2成立,故③正确;
④中,构造函数y=|x|(x+2),
(1)当x≥0时,y=x(x+2)=(x+1)2-1;(2)当x<0时,y=-x(x+2)=-(x+1)2+1,对称轴x=-1,
作出图象如图(右二):
∵方程|x|(x+2)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,即两个图象有3个交点,
∴0<m<1,
不妨设 x1<x2<x3,则x1+x2=-2,
当m=1时,x(x+2)=1,得x=-1+
| 2 |
此时x3满足0<x3<
| 2 |
∴x1+x2+x3的取值范围是(-2,
| 2 |
故答案为:③④
点评:本题考查复合函数单调性、函数的零点、指数函数与幂函数的增长规律及函数图象的对称性,考查数形结合思想,考查学生对知识掌握的全面性.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目