题目内容
给出下列说法:①函数y=
是幂函数;②若x+y≠8,则x≠2或y≠6;③命题:“矩形对角线相等”的否定是“矩形对角线不相等”;④若函数f(x)的定义域是[-1,1],则函数y=f(x2)的定义域是[0,1].其中正确的有( )
| 1 | ||
|
分析:由幂函数的概念可判断①,由命题的逆否命题及命题的否定可判断②③,由函数的性质可判断④.
解答:解:①,∵y=
=x-
,是幂函数,故①正确;
②,∵若x+y≠8,则x≠2或y≠6的逆否命题为:若x=2且y=6,则x+y=8为真命题,又命题与其逆否命题真假性一致,
故②正确;
③,“矩形对角线相等”的否定是“矩形对角线不相等”正确;
④,∵函数f(x)的定义域是[-1,1],
∴由-1≤x2≤1得,-1≤x≤1,
∴函数y=f(x2)的定义域为:{x|-1≤x≤1},故④函数y=f(x2)的定义域是[0,1]是错误的.
故选D.
| 1 | ||
|
| 1 |
| 2 |
②,∵若x+y≠8,则x≠2或y≠6的逆否命题为:若x=2且y=6,则x+y=8为真命题,又命题与其逆否命题真假性一致,
故②正确;
③,“矩形对角线相等”的否定是“矩形对角线不相等”正确;
④,∵函数f(x)的定义域是[-1,1],
∴由-1≤x2≤1得,-1≤x≤1,
∴函数y=f(x2)的定义域为:{x|-1≤x≤1},故④函数y=f(x2)的定义域是[0,1]是错误的.
故选D.
点评:本题考查命题的真假判断与应用,掌握幂函数的概念,掌握命题及其关系是判断的基础,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
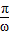 ;
;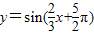 是偶函数;
是偶函数;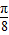 个单位长度得到
个单位长度得到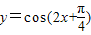 的图象.
的图象.