题目内容
给出下列说法:
①函数y=cosx在第三、四象限都是减函数;
②函数y=tan(ωx+φ)的最小正周期为
;
③函数y=sin(
x+
π)是偶函数;
④函数y=cos2x的图象向左平移
个单位长度得到y=cos(2x+
)的图象.
其中正确说法的序号是
①函数y=cosx在第三、四象限都是减函数;
②函数y=tan(ωx+φ)的最小正周期为
| π |
| ω |
③函数y=sin(
| 2 |
| 3 |
| 5 |
| 2 |
④函数y=cos2x的图象向左平移
| π |
| 8 |
| π |
| 4 |
其中正确说法的序号是
③④
③④
.分析:三角函数的增减性问题时不能把三角函数图象和单位圆里的三角函数值搞混淆了.三角函数在象限内是无限重复延伸的,故不是单调的.只有在区间内可判断单调性,可判断①,根据函数y=tan(ωx+φ)的最小正周期为
,可判断②,利用诱导公式化简函数的解析式,结合函数奇偶性的定义,可判断③,利用函数图象的平移变换法则求出平移后的函数解析式,可判断④
| π |
| |ω| |
解答:解:函数的单调性是针对象限的,而不是针对区间的,故①错误;
函数y=tan(ωx+φ)的最小正周期为
,当ω为负时,②不满足要求,故②错误;
令f(x)=y=sin(
x+
π)=cos
x,则f(-x)=cos(-
x)=cos
x=f(x),故函数为偶函数,故③正确,
函数y=cos2x的图象向左平移
个单位长度得到y=cos2(x+
)=cos(2x+
)的图象,故④正确
故正确说法的序号是③④
故答案为:
函数y=tan(ωx+φ)的最小正周期为
| π |
| |ω| |
令f(x)=y=sin(
| 2 |
| 3 |
| 5 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
函数y=cos2x的图象向左平移
| π |
| 8 |
| π |
| 8 |
| π |
| 4 |
故正确说法的序号是③④
故答案为:
点评:本题以命题的真假判断为载体考查了三角函数的单调性,周期性,奇偶性和图象平移,是三角函数问题比较综合的应用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
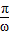 ;
;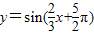 是偶函数;
是偶函数;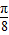 个单位长度得到
个单位长度得到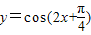 的图象.
的图象.