题目内容
【题目】如图，已知椭圆C： 
+ 
=1（a＞b＞0）的离心率为 
，短轴端点与椭圆的两个焦点所构成的三角形面积为1，过点D（0，2）且斜率为k的直线l交椭圆于A，B两点．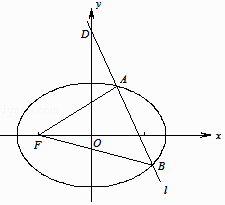 
（1）求椭圆C的方程；
（2）是否存在定点 
，使 
恒为定值．若存在求出这个定值；若不存在，说明理由．
【答案】
（1）解：根据 
，
解得 
，
椭圆C的方程为 
（2）解：设A（x1，y1），B（x2，y2），联立方程得，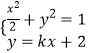 
，
消y得（1+2k2）x2+8kx+6=0，
则x1+x2=﹣ 
，x1x2= 
．
又∴y1y2=（kx1+2）（kx2+2）=k2x1x2+2k（x1+x2）+4=﹣ 
，
y1+y2=（kx1+2）+（kx2+2）=k（x1+x2）+4= 
．
∵ 
，
∴ 
= 
= 
．
故 
恒为定值 
【解析】（1）根据椭圆的性质列方程解出a，b；（2）联立方程组消元，得出A，B坐标的关系，代入向量的数量积公式计算即可．
练习册系列答案
相关题目
