题目内容
【题目】如图,在三棱锥P﹣ABC中,PA⊥PC,PB=AB=BC=2,∠ABC=120°, ![]() ,D为AC上一点,且AD=3DC.
,D为AC上一点,且AD=3DC. 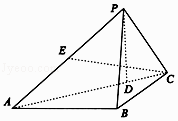
(1)求证:PD⊥平面ABC;
(2)若E为PA中点,求直线CE与平面PAB所成角的正弦值.
【答案】
(1)证明:取AC中点O,连接OP,OB,
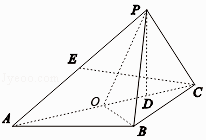
则由AD=3DC,知D为OC中点.
∵AB=BC=2,∠ABC=120°,
∴由余弦定理,得 ![]() .
.
∵PA⊥PC,∴在Rt△PAC中, ![]() ,
,
∴OP=PC,∴PD⊥AC.
又∵PB=AB=BC=2,∴OB⊥AC, ![]() ,∴OB2+OP2=PB2,∴OB⊥OP,
,∴OB2+OP2=PB2,∴OB⊥OP,
又∵OP∩AC=O,∴OB⊥平面PAC,∵PD平面PAC,∴OB⊥PD,
又∵OB∩AC=O,∴PD⊥平面ABC.
(2)解:以O为坐标原点,OA,OB所在直线分别为x,y轴,建立空间直角坐标系O﹣xyz,如图所示,
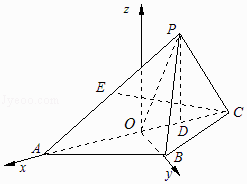
则 ![]() ,B(0,1,0),
,B(0,1,0), ![]() ,
, ![]() ,
, ![]() ,∴
,∴ ![]() ,
, ![]() ,
, ![]() .
.
设 ![]() 是平面PAB的一个法向量,则
是平面PAB的一个法向量,则
由 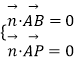 ,得
,得 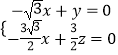 ,取x=1,则
,取x=1,则 ![]() .
.
设直线CE与平面PAB所成角为θ,则 ![]() ,
,
∴直线CE与平面PAB所成角的正弦值为 ![]() .
.
解法二:作EF⊥AC于F,则 ![]() ,
, ![]() ,
,
所以 ![]() .在△PAB中,AB=PB=2,
.在△PAB中,AB=PB=2, ![]() ,
,
所以高 ![]()
设点C到平面PAB的距离为h,则 ![]()
另一方面, ![]()
所以 ![]() ,
,
所以直线CE与平面PAB所成角的正弦值 ![]() .
.
【解析】(1)取AC中点O,连接OP,OB,证明PD⊥AC,OB⊥PD,利用线面垂直的判定定理,证明PD⊥平面ABC;(2)方法一:以O为坐标原点,OA,OB所在直线分别为x,y轴,建立空间直角坐标系,求出平面的法向量,利用向量方法求直线CE与平面PAB所成角的正弦值.方法二:作EF⊥AC于F,求出点C到平面PAB的距离,即可求直线CE与平面PAB所成角的正弦值.
【考点精析】利用直线与平面垂直的判定和空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则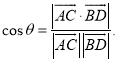 .
.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案