题目内容
(本小题满分14分)对于函数 ,若存在
,若存在 ,使
,使 成立,则称
成立,则称 为
为 的不动点。如果函数
的不动点。如果函数 有且仅有两个不动点
有且仅有两个不动点 、
、 ,且
,且 。
。
(1)试求函数 的单调区间;
的单调区间;
(2)已知各项均为负的数列 满足
满足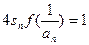 ,求证:
,求证: ;
;
(3)设 ,
, 为数列
为数列 的前
的前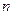 项和,求证:
项和,求证: 。
。
(1)设
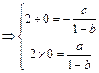 ∴
∴ ∴
∴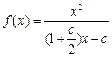
由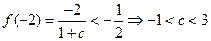
又∵ ∴
∴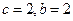 ∴
∴ …… 3分
…… 3分
于是
由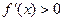 得
得 或
或 ; 由
; 由 得
得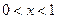 或
或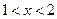
故函数 的单调递增区间为
的单调递增区间为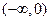 和
和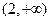 ,
,
单调减区间为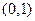 和
和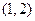 ……4分
……4分
(2)由已知可得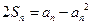 , 当
, 当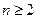 时,
时,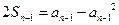
两式相减得
∴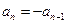 或
或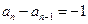
当 时,
时,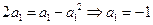 ,若
,若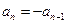 ,则
,则 这与
这与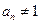 矛盾
矛盾
∴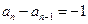 ∴
∴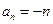 ……6分
……6分
于是,待证不等式即为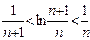 。为此,我们考虑证明不等式
。为此,我们考虑证明不等式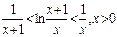
令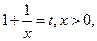 则
则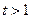 ,
,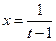
再令 ,
, 由
由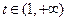 知
知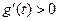
∴当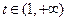 时,
时,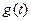 单调递增 ∴
单调递增 ∴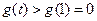 于是
于是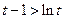
即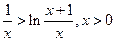 ①
①
令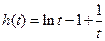 ,
,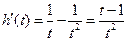 由
由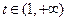 知
知
∴当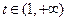 时,
时, 单调递增 ∴
单调递增 ∴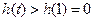 于是
于是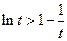
即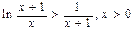 ②
②
由①、②可知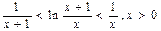 ……10分
……10分
所以,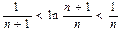 ,即
,即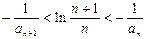 ……11分
……11分
(3)由(2)可知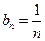 则
则
在 中令n=1,2,3…………..2010并将各式相加得
中令n=1,2,3…………..2010并将各式相加得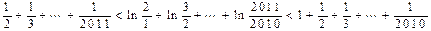
即
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
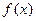 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时
时
 ,使得当
,使得当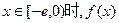 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出 .
. +
+ +2=0对定义域内的所有
+2=0对定义域内的所有 都成立;
都成立;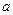 +
+ ,
, -2];
-2]; ,函数
,函数 =x2+|(x-
=x2+|(x- (
( )(
)( 为自然对数的底数)
为自然对数的底数) 的极值
的极值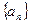 ,
, (
( )
)

 的方程
的方程 是否有解,并说明理由
是否有解,并说明理由 (e为自然对数的底)。
(e为自然对数的底)。 在其定义域为单调函数,求p的取值范围。
在其定义域为单调函数,求p的取值范围。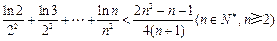 。
。 ,其中
,其中
 ,若
,若 在区间
在区间 上不是单调函数,求
上不是单调函数,求 的取值范围.
的取值范围.
 是否存在
是否存在 ,存在唯一的非零
,存在唯一的非零 使得
使得 成立,若存在,求
成立,若存在,求 资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元. 的费用为y(元)(不计返程费用),将y表示成速度v的函数
的费用为y(元)(不计返程费用),将y表示成速度v的函数 关系式;
关系式; 时,车流速度
时,车流速度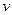 是车流密度
是车流密度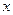 的一次函数.
的一次函数.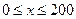 时,求函数
时,求函数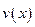 的表达式;
的表达式; (单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
(单位时间内通过桥上某观测点的车辆数,单位:辆/小时) 可以达到最大,并求出最
可以达到最大,并求出最 大值.(精确到1辆/小时)
大值.(精确到1辆/小时) 处连续的是
处连续的是