题目内容
11.已知f(x)是定义在R上且周期为3的函数,当x∈[0,3)时.f(x)=|x2-4x+3|,若函数y=f(x)-a在区间[-4,4]上有8个互不相同的零点,则实数a的取值范围是(0,1).分析 由y=f(x)-a=0得f(x)=a,利用函数f(x)的周期性,作出函数f(x)的图象,利用数形结合即可得到结论.
解答 解:由y=f(x)-a=0得f(x)=a,
∵f(x)是定义在R上且周期为3的函数,当x∈[0,3)时.f(x)=|x2-4x+3|,
∴作出函数f(x)在区间[-4,4]上的图象如图:
则当a=1时,在区间[-4,4]上两个图象有6个交点,
当a=0时,在区间[-4,4]上两个图象有3个交点,
当0<a<1时,在区间[-4,4]上两个图象有8个交点,
故若函数y=f(x)-a在区间[-4,4]上有8个互不相同的零点,则实数a的取值范围是<a<1,
故答案为:(0,1)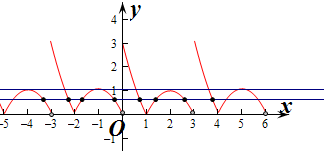
点评 本题主要考查函数方程和函数之间的关系,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
12.在2014“双11购物节”到来之际,某公司对员工在当天的网购计划进行了调查,数据绘成表格如下:
若公司准备采用分成抽样的方式抽取其中的若干人进行座谈,已知每位员工被抽到的概率均为$\frac{1}{20}$,且“计划购物1000元以上”者抽取的人数为4人,则该公司员工总数为( )
| 计划购物情况 | 没有计划购物 | 计划购物1000元以内(不含1000元) | 计划购物1000元以上(含1000元) |
| 所占比例 | $\frac{1}{5}$ | $\frac{2}{3}$ | x |
| A. | 100 | B. | 200 | C. | 300 | D. | 600 |
16.四面体ABCD的外接球为O,AD⊥平面ABC,AD=2,△ABC为边长为3的正三角形,则球O的表面积为( )
| A. | 32π | B. | 16π | C. | 12π | D. | $\frac{32}{3}$π |
3.下列函数中既是奇函数又是增函数的是( )
| A. | y=3x+1 | B. | y=2-x-2x | C. | y=x2+1 | D. | y=x|x| |
20.在△ABC中,a,b,c分别为角A,B,C所对的边,且ccosA=b,则△ABC是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 斜三角形 |
1.下列函数在(0,+∞)上为减函数的是( )
| A. | y=x | B. | y=x2 | C. | y=$\frac{1}{x}$ | D. | y=$\sqrt{x}$ |