题目内容
16. 如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.(1)证明EM⊥BF;
(2)求三棱锥E-ABF的体积.
分析 (1)根据线面垂直得到线与线垂直,根据直径所对的圆周角是直角,得到两个三角形是等腰直角三角形,有线面垂直得到结果.
(2)求出底面面积和高,由VE-ABF=VB-AEF=$\frac{1}{3}MB•{S}_{△AEF}$可得答案.
解答 (1)证明:∵EA⊥面ABC,BM?面ABC,
∴EA⊥MB
∴MB⊥AC,AC∩EA=A,
∴MB⊥面ACEF
∵EM?面ACEF,
∴EM⊥MB
在直角梯形ACEF中,EA=3,FC=1,AC=4
∴EF=2$\sqrt{5}$
在Rt△ABC中,
∵∠BAC=30°,BM⊥AC
∴AM=3,CM=1
∴EM=3$\sqrt{2}$,MF=$\sqrt{2}$
∵EF2=EM2+MF2
∴EM⊥MF,又MB∩MF=M
∴EM⊥面MBF,
∵BF?面MBF
∴EM⊥BF…(8分)
(2)解:由(1)知,MB⊥面ACFE
∴VE-ABF=VB-AEF=$\frac{1}{3}MB•{S}_{△AEF}$
在直角梯形ACEF中,${S}_{△AEF}=\frac{1}{2}AE•AC$=6,MB=$\sqrt{3}$
∴VE-ABF=2$\sqrt{3}$…(14分)
点评 本题主要考查空间点、线、面位置关系,三棱锥E-ABF的体积等基础知识,考查空间想象能力、运算能力和推理论证能力.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
 如图,A,B是椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的两个顶点,|AB|=$\sqrt{7}$,椭圆离心率为$\frac{1}{2}$.
如图,A,B是椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的两个顶点,|AB|=$\sqrt{7}$,椭圆离心率为$\frac{1}{2}$.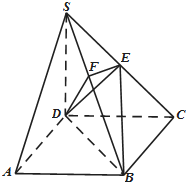 如图,在四棱锥S-ABCD中,底面ABCD是正方形,侧棱SD⊥底面ABCD,SD=DC=2,E是SC的中点,作EF⊥SB交SB于F.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,侧棱SD⊥底面ABCD,SD=DC=2,E是SC的中点,作EF⊥SB交SB于F. 如图,在△PCB中,已知∠PCB=$\frac{π}{2},∠BPC=\frac{π}{3}$,PB=4.点D为PB的中点.若△APC是△BPC绕直线PC顺时针旋转而成的,记二面角B-PC-A的大小为θ.
如图,在△PCB中,已知∠PCB=$\frac{π}{2},∠BPC=\frac{π}{3}$,PB=4.点D为PB的中点.若△APC是△BPC绕直线PC顺时针旋转而成的,记二面角B-PC-A的大小为θ. 某大型连锁超市为迎接春节购物季,销售一批年货产品,已知每销售1份获利30元,未销售的产品每份损失10元,根据以往销售情况其市场需求量的频率分布直方图如图所示,该超市欲购8000份.
某大型连锁超市为迎接春节购物季,销售一批年货产品,已知每销售1份获利30元,未销售的产品每份损失10元,根据以往销售情况其市场需求量的频率分布直方图如图所示,该超市欲购8000份.