题目内容
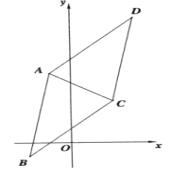
【题目】如图，在多面体ABC—DEF中，若AB//DE，BC//EF．
（1）求证：平面ABC//平面DEF；
（2）已知
是二面角C-AD-E的平面角．求证：平面ABC
平面DABE．
【答案】（1）见解析（2）见解析
【解析】分析：（1）由题意得AB//平面DEF，BC//平面DEF，利用面面平行的判定定理可得结论成立．（2）由二面角的定义可得
，于是DA
平面ABC，从而可得结论成立．
详解：（1）因为AB//DE，AB
平面DEF，DE
平面DEF，
所以AB//平面DEF，
同理BC//平面DEF，
又因为
，
平面ABC，
所以平面ABC//平面DEF．
（2）因为
是二面角C-AD-E的平面角，
所以
又因为
，
平面ABC，
所以DA平面ABC，
又DA平面DABE，
所以平面ABC平面DABE.
练习册系列答案
初中学业考试导与练系列答案
相关题目
【题目】某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
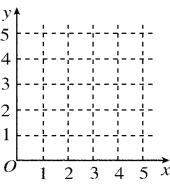
(1)在给定的坐标系中画出表中数据的散点图；
(2)求出y关于x的线性回归方程
(3)试预测加工10个零件需要多少小时？
