Question

【题目】已知复数z=（m2+5m﹣6）+（m2﹣2m﹣15）i，（i为虚数单位，m∈R）
（1）若复数Z在复平面内对应的点位于第一、三象限的角平分线上，求实数M的值；
（2）当实数m=﹣1时，求 的值．

Answer 1

【答案】
（1）解：因为复数z所对应的点在一、三象限的角平分线上，

所以m2+5m+6=m2﹣2m﹣15，

解得m=﹣3

（2）解：当实数m=﹣1时，z=（1﹣5+6）+（1+2﹣15）i=2﹣12i．

∴ ，

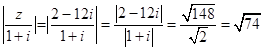所以 的值为

【解析】（1）因为复数z所对应的点在一、三象限的角平分线上，可得m2+5m+6=m2﹣2m﹣15，解得m．（2）当实数m=﹣1时，z=（1﹣5+6）+（1+2﹣15）i=2﹣12i．再利用复数的运算法则、模的计算公式即可得出．