题目内容

13．邢台一中高一某班共70人，其中39人喜欢体育课，28人喜欢音乐课，8人对这两个课程都不喜欢，则喜欢体育课但不喜欢音乐课的人数为（　　）
A．23B．34C．5D．13

分析 将条件转化为Venn图关系即可得到结论．

解答 解：设喜欢体育课又喜欢音乐课的人数为x，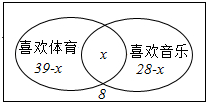

由图可得：只喜欢体育的有39-x人，只喜欢音乐的有：28-x人，
则8+（39-x）+x+（28-x）=70，
解得：x=5，
则39-x=34，
即喜欢体育课但不喜欢音乐课的人数为34人，
故选：B．

点评 本题主要考查Venn图的应用，根据条件转化为集合关系是解决本题的关键

练习册系列答案
相关题目
3．若关于x的方程$\frac{x+1}{x+2}$-$\frac{x}{x-1}$=$\frac{ax+2}{（x-1）（x+2）}$无解，求a的值为（　　）
A．-5B．-$\frac{1}{2}$C．-5或-$\frac{1}{2}$D．-5或-$\frac{1}{2}$或-2
4．某次抽奖活动在三个箱子中均放有红、黄、绿、蓝、紫、橙、白、黑8种颜色的球各一个，奖励规则如下：从三个箱子中分别摸出一个球，摸出的3 个球均为红球的得一等奖，摸出的3个球中至少有一个绿球的得二等奖，摸出的3个球均为彩色球（黑、白除外）的得三等奖．问不中奖的概率是多少？（　　）
A．在0～25%之间B．在25～50%之间C．在50～75%之间D．在75～100%之间
1．若向量$\overrightarrow{a}$=（cosα，1），$\overrightarrow{b}$=（1，2tanα），且$\overrightarrow{a}∥\overrightarrow{b}$，则sinα=$\frac{1}{2}$．
8．已知函数f（x）=2$\sqrt{3}$sin（x+$\frac{π}{4}$）cos（x+$\frac{π}{4}$）-sin（2x+π）．
（1）求f（x）的最小正周期和单调递减区间；
（2）若将f（x）的图象向右平移$\frac{π}{4}$个单位，得到函数g（x）的图象，求函数g（x）在区间[0，$\frac{π}{2}$]上的最大值和最小值．
18．集合A，B各有两个元素，A∩B中有一个元素，若集合C同时满足：（1）C⊆（A∪B），（2）C?（A∩B），则满足条件C的个数为（　　）
A．1B．2C．3D．4
5．在△ABC中，内角A，B，C的对边分别为a，b，c，面积为S，已知acos2$\frac{C}{2}$+ccos2$\frac{A}{2}$=$\frac{3}{2}$b．
（Ⅰ）求a+c-2b的值；
（Ⅱ）若B=$\frac{π}{3}$，S=4$\sqrt{3}$，求b．
2．若函数y=x2-2ax+1在（-∞，2]上是减函数，则实数a的取值范围（　　）
A．[-∞，-2]B．[-2，+∞]C．[2，+∞]D．[-∞，2]
3．已知函数f（x）=$\left\{\begin{array}{l}{\stackrel{-1}{x}}&{\stackrel{x≤-1}{-1＜x＜-1}}\\{1}&{x≥1}\end{array}\right.$，函数g（x）=ax2+$\frac{1}{4}$．若函数y=f（x）-g（x）恰有2个不同的零点，则实数a的取值范围是（　　）
A．（0，+∞）B．（-∞，0）∪（2，+∞）C．（-∞，-$\frac{1}{2}$）∪（1，+∞）D．（-∞，0）∪（0，1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网