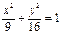题目内容
(本小题满分10分) 如图,已知椭圆C: ,经过椭圆
,经过椭圆 的右焦点F且斜率为
的右焦点F且斜率为 的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(I)是否存在
的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(I)是否存在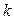 ,使对任意
,使对任意 ,总有
,总有 成立?若存在,求出所有
成立?若存在,求出所有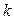 的值;
的值;
(II)若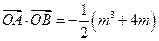 ,求实数
,求实数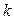 的取值范围.
的取值范围.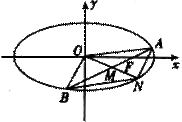
 ,经过椭圆
,经过椭圆 的右焦点F且斜率为
的右焦点F且斜率为 的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(I)是否存在
的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(I)是否存在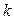 ,使对任意
,使对任意 ,总有
,总有 成立?若存在,求出所有
成立?若存在,求出所有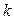 的值;
的值;(II)若
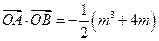 ,求实数
,求实数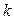 的取值范围.
的取值范围.
(1)
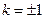
(2)
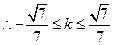 且k≠0
且k≠0解:(1)椭圆C: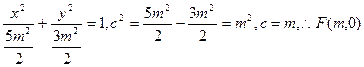
直线AB:y=k(x-m),
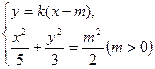 ,(10k2+6)x2-20k2mx+10k2m2-15m2=0.
,(10k2+6)x2-20k2mx+10k2m2-15m2=0.
设A(x1, y1)、B(x2,y2),则x1+x2=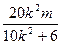 ,x1x2=
,x1x2=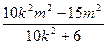
则xm=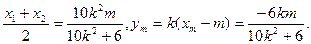
若存在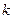 ,使
,使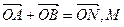 为ON的中点,∴
为ON的中点,∴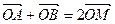 .
.
∴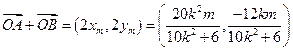 ,
,
即N点坐标为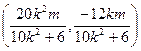 .
.
由N点在椭圆上,则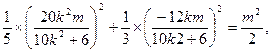
即5k4-2k2-3=0.∴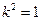 或
或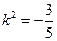 (舍).
(舍).
故存在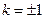 ,使
,使 .··········5分
.··········5分
(2)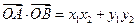 =x1x2+k2(x1-m)(x2-m)
=x1x2+k2(x1-m)(x2-m)
=(1+k2)x1x2-k2m(x1+x2)+k2m2
=(1+k2)·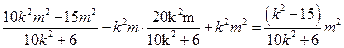
由 得
得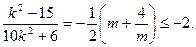
即k2-15≤-20k2-12,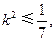
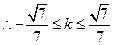 且k≠0.··········10分
且k≠0.··········10分
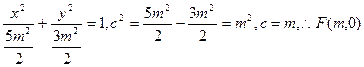
直线AB:y=k(x-m),
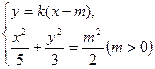 ,(10k2+6)x2-20k2mx+10k2m2-15m2=0.
,(10k2+6)x2-20k2mx+10k2m2-15m2=0. 设A(x1, y1)、B(x2,y2),则x1+x2=
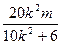 ,x1x2=
,x1x2=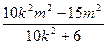
则xm=
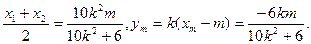
若存在
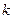 ,使
,使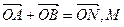 为ON的中点,∴
为ON的中点,∴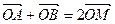 .
.∴
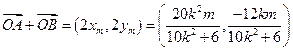 ,
,即N点坐标为
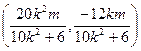 .
. 由N点在椭圆上,则
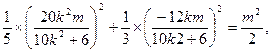
即5k4-2k2-3=0.∴
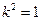 或
或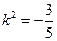 (舍).
(舍).故存在
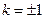 ,使
,使 .··········5分
.··········5分 (2)
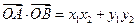 =x1x2+k2(x1-m)(x2-m)
=x1x2+k2(x1-m)(x2-m)=(1+k2)x1x2-k2m(x1+x2)+k2m2
=(1+k2)·
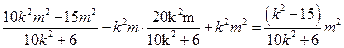
由
 得
得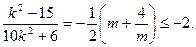
即k2-15≤-20k2-12,
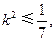
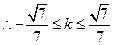 且k≠0.··········10分
且k≠0.··········10分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
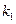 的直线
的直线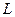 交椭圆
交椭圆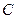 :
: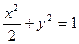 于
于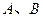 两点,点
两点,点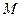 为弦
为弦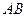 的中点,直线
的中点,直线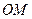 的斜率为
的斜率为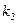 (其中
(其中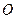 为坐标原点,假设
为坐标原点,假设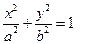 (
(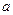 >
>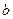 >0),其它条件不变,试猜想
>0),其它条件不变,试猜想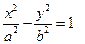 (
(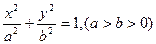 的两个焦点分别为
的两个焦点分别为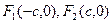 ,
,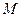 是椭圆上一点,且满足
是椭圆上一点,且满足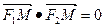 。
。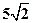 。
。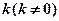 的直线l与椭圆C相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点P(0,
的直线l与椭圆C相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点P(0,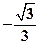 )、Q的直线对称?若能,求出
)、Q的直线对称?若能,求出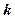 的取值范围;若不能,请说明理由。
的取值范围;若不能,请说明理由。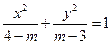 表示焦点在
表示焦点在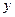 轴上的椭圆,则
轴上的椭圆,则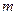 的取值范围是 .
的取值范围是 . 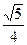

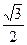
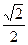
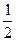
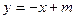 与曲线
与曲线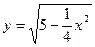 只有一个公共点,则m的取值范围是( )
只有一个公共点,则m的取值范围是( )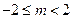
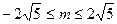
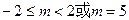
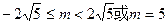
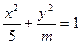 的离心率
的离心率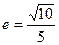 ,则
,则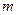 的值为 ( )
的值为 ( )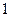
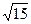 或
或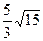
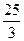
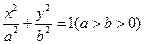 的离心率为
的离心率为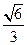 ,过
,过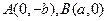 的直线与原点的距离为
的直线与原点的距离为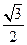
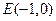 ,直线
,直线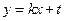 与椭圆交于不同两点C,D,试问:对任意的
与椭圆交于不同两点C,D,试问:对任意的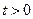 ,是否都存在实数
,是否都存在实数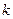 ,使得以线段CD为直径的圆过点E?证明你的结论
,使得以线段CD为直径的圆过点E?证明你的结论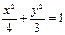 (B)
(B)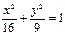 (C)
(C)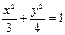 (D)
(D)