题目内容
【题目】某工厂有100名工人接受了生产1000台某产品的总任务，每台产品由9个甲型装置和3个乙型装置配套组成，每个工人每小时能加工完成1个甲型装置或3个乙型装置．现将工人分成两组分别加工甲型和乙型装置．设加工甲型装置的工人有x人，他们加工完甲型装置所需时间为
小时，其余工人加工完乙型装置所需时间为
小时，则生产1000台某产品的总加工时间y是一个关于x的函数。
（1）求y关于x的函数解析式；
（2）如何分配工人才能使生产1000台某产品的总加工时间最少？
【答案】（1）
；（2）当加工甲装置工人为
时，乙装置工人
时，总加工时间最少.
【解析】
（1）1000台产品中共有9000个甲型装置，3000个乙型装置，因此
人加工完甲型装置的时间为
，而剩下的
个加工完乙型装置的时间为
，两者相加即得总的加工时间．注意
且
；
（2）从
的表达式中可以看出，通过凑配法凑出定值后可求得最小值．
，然后应用基本不等式可求得最小值．
(1)
（2）
，
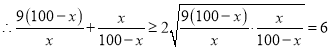
当且仅当
时，即
时等号成立，
所以，当加工甲装置工人为时，乙装置工人时，总加工时间最少.
【题目】某校为了解学生一次考试后数学、物理两个科目的成绩情况，从中随机抽取了25位考生的成绩进行统计分析．25位考生的数学成绩已经统计在茎叶图中，物理成绩如下：
（Ⅰ）请根据数据在答题卡的茎叶图中完成物理成绩统计；
（Ⅱ）请根据数据在答题卡上完成数学成绩的频数分布表及数学成绩的频率分布直方图；
数学成绩分组 | [50，60﹚ | [60，70﹚ | [70，80﹚ | [80，90﹚ | [90，100﹚ | [100，110﹚ | [110，120] |
频数 |
（Ⅲ）设上述样本中第i位考生的数学、物理成绩分别为xi，yi（i=1，2，3，…，25）．通过对样本数据进行初步处理发现：数学、物理成绩具有线性相关关系，得到：
=86，
=64，
（xi-）（yi-）=4698，（xi-）2=5524，
≈0.85．求y关于x的线性回归方程，并据此预测当某考生的数学成绩为100分时，该考生的物理成绩（精确到1分）．
附：回归直线方程的斜率和截距的最小二乘估计公式分别为：
=
，
=-
．
【题目】某酱油厂对新品种酱油进行了定价，在各超市得到售价与销售量的数据如下表：
单价 | 5 | 5.2 | 5.4 | 5.6 | 5.8 | 6 |
销量 | 9.0 | 8.4 | 8.3 | 8.0 | 7.5 | 6.8 |
（1）求售价与销售量的回归直线方程；（
，
）
（2）预计在今后的销售中，销量与单价仍然服从（1）中的关系，且该产品的成本是4元/瓶，为使工厂获得最大利润（利润=销售收入
成本），该产品的单价应定为多少元？
相关公式：
，
．
【题目】某校高一年级有学生480名，对他们进行政治面貌和性别的调查，其结果如下：
性别 | 团员 | 群众 |
男 |
| 80 |
女 | 180 |
|
（1）若随机抽取一人，是团员的概率为
，求
，
；
（2）在团员学生中，按性别用分层抽样的方法，抽取一个样本容量为5的样本，然后在这5名团员中任选2人，求两人中至多有1个女生的概率．