题目内容
2．某企业生产甲、乙两种产品．已知生产每吨甲产品要用A原料3吨、B原料2吨；生产每吨乙产品要用A原料1吨、B原料3吨．该企业在一个生产周期内消耗A原料不超过13吨、B原料不超过18吨，列出满足生产条件的关系式，并画出相应的平面区域．分析 设生产甲产品x吨，乙产品y吨，建立不等式组，即可．
解答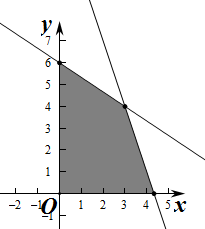 
解：设生产甲产品x吨，乙产品y吨，由题意得$\left\{\begin{array}{l}{x≥0，y≥0}\\{3x+y≤13}\\{2x+3y≤18}\end{array}\right.$，
对应的可行域如图：
点评 本题主要考查线性规划的应用题，利用条件建立二元一次不等式组是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
13．设不等式组$\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤1}\end{array}\right.$表示的平面区域为D，在区域D内随机取一个点，则此点到坐标原点的距离小于2的概率是（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π-\sqrt{3}}{6}$ | C． | $\frac{\sqrt{3}+3π}{12}$ | D． | $\frac{3\sqrt{3}+2π}{18}$ |
如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AD⊥平面PCD，PA⊥CB，AB=2AD=2CD=2，E为PB的中点
已知数列{an}中，a1=1，an+1=an+n，若利用如图所示的程序框图计算该数列的第10项的值S，则判断框内的条件是n≤9或n＜10．
14．已知实数x，y满足条件$\left\{\begin{array}{l}{x+2y-5≤0}\\{x+y-3≥0}\\{y-1≥0}\end{array}\right.$，则目标函数z=$\frac{y}{x}$+$\frac{x}{y}$的取值范围为（ ）
| A． | [2，$\frac{5}{2}$] | B． | [$\frac{5}{2}$，$\frac{10}{3}$] | C． | [2，$\frac{10}{3}$] | D． | [$\frac{1}{3}$，2] |
11．设a=$\frac{200{7}^{\frac{1}{n}}-200{7}^{-\frac{1}{n}}}{2}$（n∈N*），那么（$\sqrt{1+{a}^{2}}$-a）n的结果是（ ）
| A． | 2007-1 | B． | -2007-1 | C． | （-1）n•2007 | D． | （-1）n•2007-1 |
12．直线l与直线x-$\sqrt{3}$y+1=0垂直，则直线l的斜率为（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | -$\frac{\sqrt{3}}{3}$ | C． | $\sqrt{3}$ | D． | -$\sqrt{3}$ |