题目内容
曲线y=sin(x- )(0≤x≤
)(0≤x≤ )与坐标轴围成的面积是________.
)与坐标轴围成的面积是________.

分析:将y=sin(x-
 )展开,得当0<x<
)展开,得当0<x< 时,函数值为负数;当
时,函数值为负数;当 <x<
<x< 时,函数值为负数.因此所求图形的面积为函数y=-sin(x-
时,函数值为负数.因此所求图形的面积为函数y=-sin(x- )在区间[0,
)在区间[0, ]上的积分值,加上y=sin(x-
]上的积分值,加上y=sin(x- )在区间[
)在区间[ ,
, ]上的积分值所得的和.最后根据积分的计算公式和运算法则加以计算,可得所求图形的面积.
]上的积分值所得的和.最后根据积分的计算公式和运算法则加以计算,可得所求图形的面积.解答:∵y=sin(x-
 )=sinxcos
)=sinxcos -cosxsin
-cosxsin =
= (sinx-cosx)
(sinx-cosx)
∴当0<x<
 时,sinx<cosx,函数值为负数;
时,sinx<cosx,函数值为负数;当
 <x<
<x< 时,sinx>cosx,函数值为正数.
时,sinx>cosx,函数值为正数.因此,所求图形的面积为
S=
 [-sin(x-
[-sin(x- )]dx+
)]dx+ sin(x-
sin(x- )dx
)dx=
 [
[ (-sinx+cosx)dx+
(-sinx+cosx)dx+ (sinx-cosx)]dx
(sinx-cosx)]dx=
 [(cosx+sinx)
[(cosx+sinx)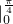 +(-cosx-sinx)
+(-cosx-sinx)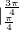 ]
]=
 [(
[( )-(-
)-(- )]=
)]=
故答案为:

点评:本题求函数在指定区间上的图象与坐标轴围成的面积,着重考查了定积分的计算公式和运算法则,以及三角函数恒等变形等知识,属于基础题.

练习册系列答案
相关题目
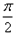 x)与y=x3在区间[0,1]上所围成的图形面积为( )。
x)与y=x3在区间[0,1]上所围成的图形面积为( )。