题目内容
曲线y=sin(x-
)(0≤x≤
)与坐标轴围成的面积是
| π |
| 4 |
| 3π |
| 4 |
2-
| ||
| 2 |
2-
.
| ||
| 2 |
分析:将y=sin(x-
)展开,得当0<x<
时,函数值为负数;当
<x<
时,函数值为负数.因此所求图形的面积为函数y=-sin(x-
)在区间[0,
]上的积分值,加上y=sin(x-
)在区间[
,
]上的积分值所得的和.最后根据积分的计算公式和运算法则加以计算,可得所求图形的面积.
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
解答:解:∵y=sin(x-
)=sinxcos
-cosxsin
=
(sinx-cosx)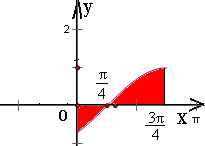
∴当0<x<
时,sinx<cosx,函数值为负数;
当
<x<
时,sinx>cosx,函数值为正数.
因此,所求图形的面积为
S=
[-sin(x-
)]dx+
sin(x-
)dx
=
[
(-sinx+cosx)dx+
(sinx-cosx)]dx
=
[(cosx+sinx)
+(-cosx-sinx)
]
=
[(
-1)-(-
)]=2-
故答案为:2-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |

∴当0<x<
| π |
| 4 |
当
| π |
| 4 |
| 3π |
| 4 |
因此,所求图形的面积为
S=
| ∫ |
0 |
| π |
| 4 |
| ∫ |
|
| π |
| 4 |
=
| ||
| 2 |
| ∫ |
0 |
| ∫ |
|
=
| ||
| 2 |
| | |
0 |
| | |
|
=
| ||
| 2 |
| 2 |
| 2 |
| ||
| 2 |
故答案为:2-
| ||
| 2 |
点评:本题求函数在指定区间上的图象与坐标轴围成的面积,着重考查了定积分的计算公式和运算法则,以及三角函数恒等变形等知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 )(0≤x≤
)(0≤x≤ )与坐标轴围成的面积是________.
)与坐标轴围成的面积是________.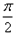 x)与y=x3在区间[0,1]上所围成的图形面积为( )。
x)与y=x3在区间[0,1]上所围成的图形面积为( )。