题目内容
16.如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,P为椭圆C上任意一点.
(1)当PF1⊥PF2时,PF1=$\sqrt{2}$,且PF2所在的弦|PQ|=$\frac{4\sqrt{2}}{3}$,求椭圆C的方程.
(2)若EF为圆N:x2+(y-2)2=1的任意一条直径,请求$\overrightarrow{PE}$•$\overrightarrow{PF}$的最大值.
分析 (1)可连接QF1,根据条件便可求出$Q{F}_{1}=\frac{5\sqrt{2}}{3}$,从而由PF1+PQ+QF1=4a便可得出a的值,而根据离心率为$\frac{\sqrt{2}}{2}$又可求出c,从而求出b,这样便可得出椭圆的方程;
(2)根据条件知N(0,2),可设P(x,y),从而可以求出${\overrightarrow{NP}}^{2}=-\frac{{c}^{2}}{{b}^{2}}•{y}^{2}-4y+4+{a}^{2}$,而根据向量减法的几何意义及EF为圆的直径便可得到$\overrightarrow{PE}•\overrightarrow{PF}={\overrightarrow{NP}}^{2}-1$,再根据离心率为$\frac{\sqrt{2}}{2}$可以得到b=c,从而得出$\overrightarrow{PE}•\overrightarrow{PF}=-{y}^{2}-4y+3+{a}^{2}$,这样通过配方便可求出$\overrightarrow{PE}•\overrightarrow{PF}$的最大值.
解答 解:(1)如图,连接QF1;
∵PF1⊥PF2,$P{F}_{1}=\sqrt{2}$,$PQ=\frac{4\sqrt{2}}{3}$;
∴$Q{F}_{1}=\frac{5\sqrt{2}}{3}$;
∵PF1+PF2+QF1+QF2=4a;
∴$\sqrt{2}+\frac{4\sqrt{2}}{3}+\frac{5\sqrt{2}}{3}=4a$;
∴$a=\sqrt{2}$;
又$\frac{c}{a}=\frac{\sqrt{2}}{2}$;
∴$c=\frac{\sqrt{2}}{2}a=1$;
∴b2=1;
∴椭圆C的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)由题意可得,N(0,2),设P(x,y),则:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$;
∴${x}^{2}={a}^{2}-\frac{{a}^{2}}{{b}^{2}}•{y}^{2}$;
∴${\overrightarrow{NP}}^{2}={x}^{2}+(y-2)^{2}$=$-\frac{{c}^{2}}{{b}^{2}}•{y}^{2}-4y+4+{a}^{2}$;
∴$\overrightarrow{PE}•\overrightarrow{PF}=(\overrightarrow{NE}-\overrightarrow{NP})•(\overrightarrow{NF}-\overrightarrow{NP})$=$(-\overrightarrow{NF}-\overrightarrow{NP})•(\overrightarrow{NF}-\overrightarrow{NP})$
=${\overrightarrow{NP}}^{2}-{\overrightarrow{NF}}^{2}={\overrightarrow{NP}}^{2}-1$=$-\frac{{c}^{2}}{{b}^{2}}•{y}^{2}-4y+3+{a}^{2}$;
∵$\frac{c}{a}=\frac{\sqrt{2}}{2}$;
∴$a=\sqrt{2}c$;
∴b2=c2;
∴$\overrightarrow{PE}•\overrightarrow{PF}=-{y}^{2}-4y+3+{a}^{2}$=-(y+2)2+7+a2;
∴y=-2时,$\overrightarrow{PE}•\overrightarrow{PF}$取得最大值7+a2.
点评 考查椭圆的标准方程,椭圆的离心率,以及椭圆的焦点,椭圆的定义,圆的标准方程,向量减法的几何意义,向量数量积的运算,相反向量的概念,以及配方求二次函数最值的方法.

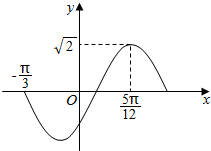 已知函数f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.