题目内容
已知椭圆C: =1(a>b>0)过点P(-1,-1),c为椭圆的半焦距,且c=
=1(a>b>0)过点P(-1,-1),c为椭圆的半焦距,且c= b.过点P作两条互相垂直的直线l1,l2与椭圆C分别交于另两点M,N.
b.过点P作两条互相垂直的直线l1,l2与椭圆C分别交于另两点M,N.
(1)求椭圆C的方程;
(2)若直线l1的斜率为-1,求△PMN的面积;
(3)若线段MN的中点在x轴上,求直线MN的方程.
(1)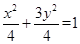 ;(2)2;(3)
;(2)2;(3)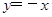 或
或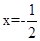 .
.
解析试题分析:(1)根据题意可得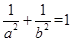 ,且
,且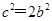 ,加之
,加之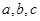 的关系,可求得
的关系,可求得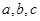 ; (2)由于直线
; (2)由于直线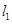 的斜率已确定,则可由其与椭圆方程联立方程组,求出点M的坐标,因两直线垂直,故当
的斜率已确定,则可由其与椭圆方程联立方程组,求出点M的坐标,因两直线垂直,故当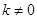 时,用
时,用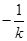 代替
代替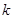 ,进而求出点N的坐标,得
,进而求出点N的坐标,得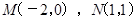 ,再由两点间的距离公式求出:
,再由两点间的距离公式求出: 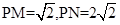 ,即可求出
,即可求出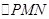 的面积;(3)观察本题条件可用设而不求的方法处理此题,即设出点
的面积;(3)观察本题条件可用设而不求的方法处理此题,即设出点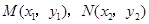 ,两点均在椭圆上得:
,两点均在椭圆上得: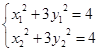 ,观察此两式的结构特征是一致的,则将两式相减得
,观察此两式的结构特征是一致的,则将两式相减得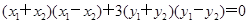 , 由题中条件线段
, 由题中条件线段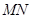 的中点在x轴上,所以
的中点在x轴上,所以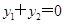 ,从而可得
,从而可得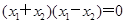 ,此式表明两点横坐标的关系:可能相等;可能互为相反数,分两种情况分类讨论:当
,此式表明两点横坐标的关系:可能相等;可能互为相反数,分两种情况分类讨论:当 时,再利用
时,再利用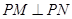 ,可转化为
,可转化为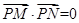 ,进一步确定出两点的坐标
,进一步确定出两点的坐标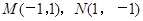 或
或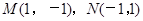 ,即可求出直线
,即可求出直线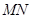 的方程为
的方程为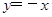 ;同理当
;同理当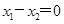 ,求出直线
,求出直线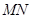 的方程为
的方程为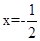 .
.
试题解析:(1)由条件得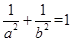 ,且
,且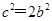 ,所以
,所以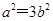 ,解得
,解得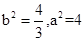 .
.
所以椭圆方程为: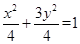 . 3分
. 3分
(2)设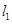 方程为
方程为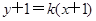 ,
,
联立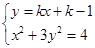 ,消去
,消去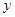 得
得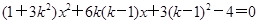 .
.
因为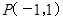 ,解得
,解得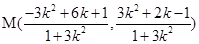 .5分
.5分
当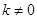 时,用
时,用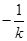 代替
代替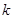 ,得
,得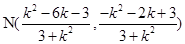 . 7分
. 7分
将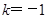 代入,得
代入,得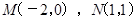 .
.
因为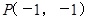 ,所以
,所以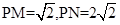 ,
,
所以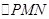 的面积为
的面积为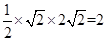 . 9分
. 9分
(3)设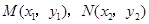 ,则
,则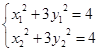 两式相减得
两式相减得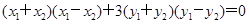 ,
,
因为线段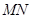 的中点在x轴上,所以
的中点在x轴上,所以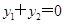 ,从而可得
,从而可得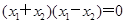 .12分
.12分
若 ,则
,则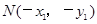 .
.
因为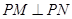 ,所以
,所以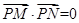

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
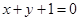 的倾斜角是 .
的倾斜角是 . 分别是椭圆
分别是椭圆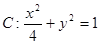 的上下两个顶点,
的上下两个顶点, 为椭圆
为椭圆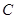 上任意一点(不与点
上任意一点(不与点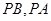 分别交
分别交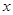 轴于
轴于 两点,若椭圆
两点,若椭圆 点,则
点,则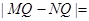 .
.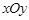 中,若圆
中,若圆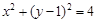 上存在
上存在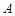 ,
,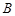 两点,且弦
两点,且弦 的中点为
的中点为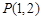 ,则直线
,则直线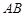 的方程为 .
的方程为 . 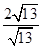 ,则
,则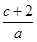 的值为________.
的值为________.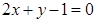 的倾斜角为
的倾斜角为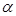 ,则
,则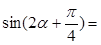 ___________.
___________.