题目内容
(2011•遂宁二模)设抛物线y2=x的焦点为F,过点M(2,0)的直线与抛物线相交于A、B两点,与抛物线的准线相交于点C,|BF|=
,则△BCF与△ACF的面积之比
=( )
| 5 |
| 4 |
| S△BCF |
| S△ACF |
分析:利用三角形面积公式,可把△BCF与△ACF的面积之比转化为BC长与AC长的比,再根据抛物线的焦半径公式借助|BF|=
求出B点坐标,得到AB方程,代入抛物线方程,解出A点坐标,就可求出BC与AC的长度之比,得到所需问题的解.
| 5 |
| 4 |
解答: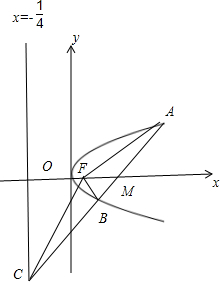 解:∵抛物线方程y2=x的焦点为F坐标为(
解:∵抛物线方程y2=x的焦点为F坐标为(
,0),准线方程为x=-
设A(x1,y1),B(x2,y2),则|BF|=x2+
=
,
∴x2=1
把x2=1代入抛物线y2=x得,结合图象以y2=1即B(1,-1)为例进行研究
∴直线AB的方程为x-y-2=0,C(-
,-
)
联立直线与抛物线方程可得
可得A(4,2)
∴|BC|=
=
|AC|=
=
∴
=
=
=
故选A
 解:∵抛物线方程y2=x的焦点为F坐标为(
解:∵抛物线方程y2=x的焦点为F坐标为(| 1 |
| 4 |
| 1 |
| 4 |
设A(x1,y1),B(x2,y2),则|BF|=x2+
| 1 |
| 4 |
| 5 |
| 4 |
∴x2=1
把x2=1代入抛物线y2=x得,结合图象以y2=1即B(1,-1)为例进行研究
∴直线AB的方程为x-y-2=0,C(-
| 1 |
| 4 |
| 9 |
| 4 |
联立直线与抛物线方程可得
|
∴|BC|=
(1+
|
5
| ||
| 4 |
|AC|=
(4+
|
17
| ||
| 4 |
∴
| S△BCF |
| S△ACF |
| ||
|
| |BC| |
| |AC| |
| 5 |
| 17 |
故选A
点评:本题主要考查了抛物线的焦半径公式,侧重了学生的转化能力,以及计算能力.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目