题目内容
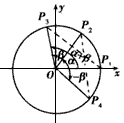
(Ⅰ)①证明两角和的余弦公式C(α+β):cos(α+β)=cosαcosβ-sinαsinβ;
②由C(α+β)推导两角和的正弦公式S(α+β):sin(α+β)=sinαcosβ+cosαsinβ;
(Ⅱ)已知△ABC的面积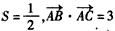 ,且
,且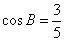 ,求cosC。
,求cosC。
②由C(α+β)推导两角和的正弦公式S(α+β):sin(α+β)=sinαcosβ+cosαsinβ;
(Ⅱ)已知△ABC的面积
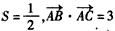 ,且
,且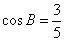 ,求cosC。
,求cosC。 | (Ⅰ)证明:①如图,在直角坐标系xOy内作单位圆O,并作出角α、β与-β, 使角α的始边为Ox,交⊙O于点P1,终边交⊙O于点P2; 角β的始边为OP2,终边交⊙O于点P3,角-β的始边为OP1,终边交⊙于点P4, 则P1(1,0),P2(cosα,sinα),  , ,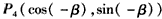 , ,由P1P3=P2P4及两点间的距离公式,则 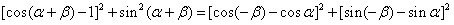 , ,展开并整理,得 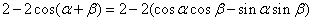 , ,∴cos(α+β)= cosαcosβ-sinαsinβ; ②由①易得, 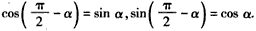 , ,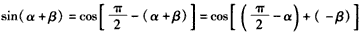 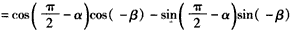 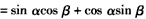 , ,∴ 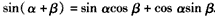 。 。 |
 |
| (Ⅱ)解:由题意,设△ABC的角B、C的对边分别为b、c, 则 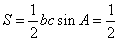 , ,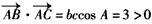 , ,∴ 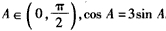 , ,又 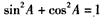 , ,∴ 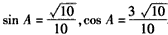 , ,由题意 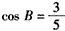 ,得 ,得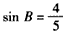 , ,∴  , ,故 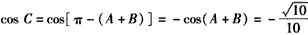 。 。 |

练习册系列答案
相关题目