题目内容
(1)证明两角和的余弦公式Cα+β:cos(α+β)=cosαcosβ-sinαsinβ;
(2)已知△ABC的面积S=
,
•
=3,且cosB=
,求cosC.
(2)已知△ABC的面积S=
| 1 |
| 2 |
| AB |
| AC |
| 3 |
| 5 |
分析:(1)如图,在直角坐标系xOy内做单位圆O,并作出角α、β与-β,使角α的始边为Ox,交⊙O于点P1,终边交⊙O于P2;角β的始边为OP2,终边交⊙O于P3;角-β的始边为OP1,终边交⊙O于P4.可得P1,P2,P3,P4的坐标,利用P1P3=P2P4及两点间的距离公式,即可证得结论.
(2)由S=
bcsinA=
>0,
•
=bccosA=3可求得sinA=
,cosA=
,又cosB=
,可求得sinB=
,利用两角和的余弦即可求得cosC.
(2)由S=
| 1 |
| 2 |
| 1 |
| 2 |
| AB |
| AC |
| ||
| 10 |
3
| ||
| 10 |
| 3 |
| 5 |
| 4 |
| 5 |
解答: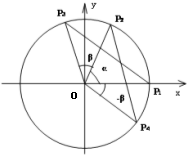 解:(1)如图,在直角坐标系xOy内做单位圆O,并作出角α、β与-β,使角α的始边为Ox,交⊙O于点P1,终边交⊙O于P2;角β的始边为OP2,终边交⊙O于P3;角-β的始边为OP1,终边交⊙O于P4.
解:(1)如图,在直角坐标系xOy内做单位圆O,并作出角α、β与-β,使角α的始边为Ox,交⊙O于点P1,终边交⊙O于P2;角β的始边为OP2,终边交⊙O于P3;角-β的始边为OP1,终边交⊙O于P4.
则P1(1,0),P2(cosα,sinα),
P3(cos(α+β),sin(α+β)),P4(cos(-β),sin(-β)) …(4分)
由P1P3=P2P4及两点间的距离公式,得
[cos(α+β)-1]2+sin2(α+β)=[cos(-β)-cosα]2+[sin(-β)-sinα]2…(6分)
展开并整理得:2-2cos(α+β)=2-2(cosαcosβ-sinαsinβ)
∴cos(α+β)=cosαcosβ-sinαsinβ.…(8分)
(2)由题意,设△ABC的角B、C的对边分别为b、c
则S=
bcsinA=
>0,
•
=bccosA=3>0
∴A∈(0,
),cosA=3sinA
又sin2A+cos2A=1,
∴sinA=
,cosA=
…(10分)
由题意,cosB=
,sinB=
…(11分)
∴cos(A+B)=cosAcosB-sinAsinB=
,
故cosC=cos[π-(A+B)]=-cos(A+B)=-
…(14分)
 解:(1)如图,在直角坐标系xOy内做单位圆O,并作出角α、β与-β,使角α的始边为Ox,交⊙O于点P1,终边交⊙O于P2;角β的始边为OP2,终边交⊙O于P3;角-β的始边为OP1,终边交⊙O于P4.
解:(1)如图,在直角坐标系xOy内做单位圆O,并作出角α、β与-β,使角α的始边为Ox,交⊙O于点P1,终边交⊙O于P2;角β的始边为OP2,终边交⊙O于P3;角-β的始边为OP1,终边交⊙O于P4.则P1(1,0),P2(cosα,sinα),
P3(cos(α+β),sin(α+β)),P4(cos(-β),sin(-β)) …(4分)
由P1P3=P2P4及两点间的距离公式,得
[cos(α+β)-1]2+sin2(α+β)=[cos(-β)-cosα]2+[sin(-β)-sinα]2…(6分)
展开并整理得:2-2cos(α+β)=2-2(cosαcosβ-sinαsinβ)
∴cos(α+β)=cosαcosβ-sinαsinβ.…(8分)
(2)由题意,设△ABC的角B、C的对边分别为b、c
则S=
| 1 |
| 2 |
| 1 |
| 2 |
| AB |
| AC |
∴A∈(0,
| π |
| 2 |
又sin2A+cos2A=1,
∴sinA=
| ||
| 10 |
3
| ||
| 10 |
由题意,cosB=
| 3 |
| 5 |
| 4 |
| 5 |
∴cos(A+B)=cosAcosB-sinAsinB=
| ||
| 10 |
故cosC=cos[π-(A+B)]=-cos(A+B)=-
| ||
| 10 |
点评:本题考查两角和与差的余弦函数,考查平面向量数量积的运算,利用任意角的三角函数的定义证明两角和的余弦公式Cα+β是难点,属于中档题.

练习册系列答案
相关题目
 ,
,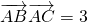 ,且
,且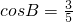 ,求cosC.
,求cosC. ,
, ,且
,且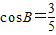 ,求cosC.
,求cosC.