题目内容
(Ⅰ)①证明两角和的余弦公式Cα+β:cos(α+β)=cosαcosβ-sinαsinβ;②由Cα+β推导两角和的正弦公式Sα+β:sin(α+β)=sinαcosβ+cosαsinβ.(Ⅱ)已知△ABC的面积S=
| 1 |
| 2 |
| AB |
| AC |
| 3 |
| 5 |
分析:(Ⅰ)①建立单位圆,在单位圆中作出角,找出相应的单位圆上的点的坐标,由两点间距离公式建立方程化简整理既得;②由诱导公式cos[
-(α+β)]=sin(α+β)变形整理可得.
(Ⅱ)S=
,
•
=3,求出角A的正弦,再由cosB=
,用cosC=-cos(A+B)求解即可.
| π |
| 2 |
(Ⅱ)S=
| 1 |
| 2 |
| AB |
| AC |
| 3 |
| 5 |
解答:解:(Ⅰ)①如图,在直角坐标系xOy内做单位圆O,并作出角α、β与-β,使角α的始边为Ox,交⊙O于点P1,
终边交⊙O于P2;
角β的始边为OP2,终边交⊙O于P3;角-β的始边为OP1,终边交⊙O于P4.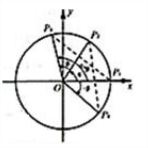
则P1(1,0),P2(cosα,sinα)
P3(cos(α+β),sin(α+β)),P4(cos(-β),sin(-β))
由P1P3=P2P4及两点间的距离公式,得
[cos(α+β)-1]2+sin2(α+β)=[cos(-β)-cosα]2+[sin(-β)-sinα]2
展开并整理得:2-2cos(α+β)=2-2(cosαcosβ-sinαsinβ)
∴cos(α+β)=cosαcosβ-sinαsinβ.(4分)
②由①易得cos(
-α)=sinα,sin(
-α)=cosα
sin(α+β)=cos[
-(α+β)]=cos[(
-α)+(-β)]
=cos(
-α)cos(-β)-sin(
-α)sin(-β)
=sinαcosβ+cosαsinβ(6分)
(Ⅱ)由题意,设△ABC的角B、C的对边分别为b、c
则S=
bcsinA=
•
=bccosA=3>0
∴A∈(0,
),cosA=3sinA
又sin2A+cos2A=1,∴sinA=
,cosA=
由题意,cosB=
,得sinB=
∴cos(A+B)=cosAcosB-sinAsinB=
故cosC=cos[π-(A+B)]=-cos(A+B)=-
(12分)
终边交⊙O于P2;
角β的始边为OP2,终边交⊙O于P3;角-β的始边为OP1,终边交⊙O于P4.

则P1(1,0),P2(cosα,sinα)
P3(cos(α+β),sin(α+β)),P4(cos(-β),sin(-β))
由P1P3=P2P4及两点间的距离公式,得
[cos(α+β)-1]2+sin2(α+β)=[cos(-β)-cosα]2+[sin(-β)-sinα]2
展开并整理得:2-2cos(α+β)=2-2(cosαcosβ-sinαsinβ)
∴cos(α+β)=cosαcosβ-sinαsinβ.(4分)
②由①易得cos(
| π |
| 2 |
| π |
| 2 |
sin(α+β)=cos[
| π |
| 2 |
| π |
| 2 |
=cos(
| π |
| 2 |
| π |
| 2 |
=sinαcosβ+cosαsinβ(6分)
(Ⅱ)由题意,设△ABC的角B、C的对边分别为b、c
则S=
| 1 |
| 2 |
| 1 |
| 2 |
| AB |
| AC |
∴A∈(0,
| π |
| 2 |
又sin2A+cos2A=1,∴sinA=
| ||
| 10 |
3
| ||
| 10 |
由题意,cosB=
| 3 |
| 5 |
| 4 |
| 5 |
∴cos(A+B)=cosAcosB-sinAsinB=
| ||
| 10 |
故cosC=cos[π-(A+B)]=-cos(A+B)=-
| ||
| 10 |
点评:本小题主要考查两角和的正、余弦公式、诱导公式、同角三角函数间的关系等基础知识及运算能力.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
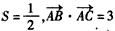 ,且
,且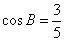 ,求cosC。
,求cosC。