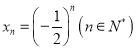题目内容
【题目】已知函数![]() .
.
(1)求![]() 的单调性;
的单调性;
(2)若对定义域内任意的![]() ,
,![]() 都恒成立,求a的取值范围;
都恒成立,求a的取值范围;
(3)记![]() ,若
,若![]() 在区间
在区间![]() 内有2个零点,求a的取值范围.
内有2个零点,求a的取值范围.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先求导得![]() ,按
,按![]() ,
,![]() ,
,![]() 分类讨论即可;
分类讨论即可;
(2)由(1)得函数![]() 的最小值,只要最小值不小于
的最小值,只要最小值不小于![]() 即可解出a的范围;
即可解出a的范围;
(3)化简得![]() ,求导得
,求导得![]() ,按
,按![]() ,
,![]() ,
,![]() 分类讨论得
分类讨论得![]() 的单调性,根据题意即可求出a的范围.
的单调性,根据题意即可求出a的范围.
(1)![]() 的定义域为
的定义域为![]() ,
,![]()
当![]() 时,
时,![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增.
上单调递增.
(2)由(1)知:当![]() 时,
时,![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 恒成立;
恒成立;
当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增,
上单调递增,
所以![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增,
上单调递增,
所以![]() ,解得
,解得![]()
综上:![]()
(3)记![]() ,化简得
,化简得![]() ,
,![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上递增,不符合题意,舍去;
上递增,不符合题意,舍去;
当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增,要使
上单调递增,要使![]() 在区间
在区间![]() 内有2个零点,
内有2个零点,
 ,解得
,解得![]() ;
;
当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增,要使
上单调递增,要使![]() 在区间
在区间![]() 内有2个零点,
内有2个零点,
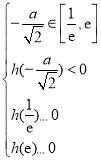 ,解得
,解得![]() ;
;
综上:![]() .
.

练习册系列答案
相关题目
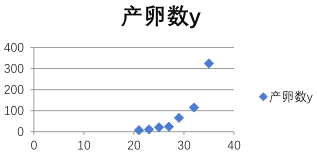
【题目】只红铃虫的产卵数y和温度x有关,现收集了7组观测数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
27 | 81 | 3.6 | 152 | 2936 | 38 |
其中![]()
(1)根据散点图判断,![]() 与
与![]() (e为自然对数的底数
(e为自然对数的底数![]() )哪一个更适宜作为红铃虫的产卵数y和温度x的回归方程类型?(给出判断即可,不必说明理由)
)哪一个更适宜作为红铃虫的产卵数y和温度x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)根据(2)的结果,当温度为37度时红铃虫的产卵数y的预报值是多少?
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其线性回归方程
,其线性回归方程![]() 的系数的最小二乘法估计值为
的系数的最小二乘法估计值为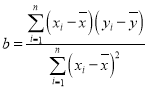 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]()