题目内容
在数列{an}中,a1=1,an+1=an+2,则a1与a5的等比中项为( )
| A.3 | B.-3 | C.±3 | D.±9 |
因为数列{an}满足an+1=an+2,则an+1-an=2,
所以数列{an}是公差为2等差数列,又a1=1,
所以,an=a1+(n-1)d=1+(n-1)×2=2n-1.
所以,a5=2×5-1=9.
设a1与a5的等比中项为m,
则m2=a1a5=1×9=9,
所以,m=±3.
故选C.
所以数列{an}是公差为2等差数列,又a1=1,
所以,an=a1+(n-1)d=1+(n-1)×2=2n-1.
所以,a5=2×5-1=9.
设a1与a5的等比中项为m,
则m2=a1a5=1×9=9,
所以,m=±3.
故选C.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
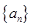 中,若
中,若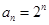 ,则
,则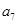 与
与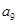 的等比中项为( )
的等比中项为( )

