题目内容
设p: ,q:关于x的不等式x2-4x+m2≤0的解集是空集,试确定实数m的取值范围,使得p或q为真命题,p且q为假命题
,q:关于x的不等式x2-4x+m2≤0的解集是空集,试确定实数m的取值范围,使得p或q为真命题,p且q为假命题
(-∞,-2)∪[0,2]∪[3,+∞)
解析试题分析:首先将命题 分别化成两个集合
分别化成两个集合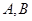 ,因为得
,因为得 或
或 为真命题,
为真命题, 且
且 为假命题,则两命题中有且只有一个命题为真,所以
为假命题,则两命题中有且只有一个命题为真,所以 的取值集合为:
的取值集合为:
试题解析: 化为
化为 ,∴0≤m<3. 4分
,∴0≤m<3. 4分
∵不等式x2-4x+m2≤0的解集为∅,∴Δ=16-4m2<0,∴m<-2或m>2. 6分
∵p或q真,p且q假,∴p与q有且仅有一真.
当p成立而q不成立时,0≤m≤2.
当p不成立而q成立时,m<-2或m≥3.
综上所述,m∈(-∞,-2)∪[0,2]∪[3,+∞). 12分
考点:1、命题与逻辑联结词;2、分式不等式的解法;3、集合的运算.

练习册系列答案
相关题目
 为不超过实数
为不超过实数 的最大整数,例如,
的最大整数,例如, ,
, ,
, 。设
。设 为正整数,数列
为正整数,数列 满足
满足 ,
, ,现有下列命题:
,现有下列命题:  时,数列
时,数列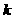 ,当
,当 时总有
时总有 ;
; 时,
时, ;
; ,则
,则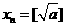 。
。 ,若
,若 同时为假命题,求x的取值集合.
同时为假命题,求x的取值集合. :方程
:方程 有两个不相等的负实根,命题
有两个不相等的负实根,命题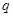 :
:
 恒成立;若
恒成立;若 的取值范围.
的取值范围. :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线。命题
轴上的双曲线。命题 曲线
曲线 与
与 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数 的取值范围。
的取值范围。 的定义域为R; q:不等式
的定义域为R; q:不等式 ,对
,对
 ∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数
∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数 的取值范围.
的取值范围. 方程
方程 在[-1,1]上有解;命题
在[-1,1]上有解;命题 只有一个实数
只有一个实数 满足不等式
满足不等式 ,若命题“p∨q”是假命题,求实数
,若命题“p∨q”是假命题,求实数 的取值范围.
的取值范围.