题目内容
已知命题 :方程
:方程 有两个不相等的负实根,命题
有两个不相等的负实根,命题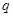 :
:
 恒成立;若
恒成立;若 或
或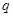 为真,
为真, 且
且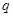 为假,求实数
为假,求实数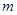 的取值范围.
的取值范围.
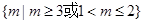 .
.
解析试题分析:先分别确定 真、
真、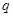 真时
真时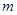 的取值范围:当
的取值范围:当 真时,只须求解不等式组
真时,只须求解不等式组 即可;当
即可;当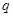 真时,只须求解不等式
真时,只须求解不等式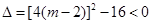 即可;然后由
即可;然后由 或
或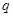 为真,
为真, 且
且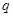 为假得到
为假得到 真
真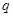 假或
假或 假
假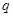 真,进而列出不等式组即可求出满足要求的
真,进而列出不等式组即可求出满足要求的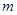 的取值范围.
的取值范围.
试题解析:当 真时,可得
真时,可得 ,解之得
,解之得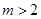
当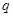 真时,得到:
真时,得到: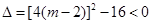 ,解之得
,解之得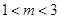
∵ 或
或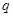 为真,
为真, 且
且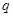 为假
为假
∴ 真
真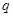 假或
假或 假
假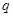 真
真
若 真
真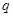 假时,由
假时,由
若 假
假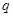 真时,由
真时,由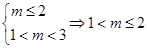
所以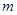 的取值范围为
的取值范围为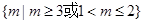 .
.
考点:1.逻辑联结词;2.二次方程根的分布问题;3.二次函数的图像与性质.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
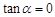 ,且
,且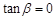 ”是“
”是“ ”成立的 ▲ 条件.(在“充分不必要”、“必要不充分”、“充分必要”、“既不充分也不必要”中选填一种)
”成立的 ▲ 条件.(在“充分不必要”、“必要不充分”、“充分必要”、“既不充分也不必要”中选填一种)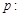 函数
函数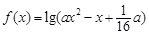 的定义域为R,命题
的定义域为R,命题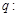 不等式
不等式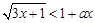 对一切正实数x均成立,如果命题
对一切正实数x均成立,如果命题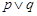 为真,
为真,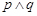 为假,求实数a的取值范围.
为假,求实数a的取值范围. ,命题
,命题 。
。 ”为真命题,“
”为真命题,“ ”为假命题,求实数x的取值范围。
”为假命题,求实数x的取值范围。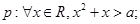 命题
命题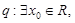
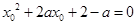 ,如果命题
,如果命题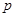 真且命题
真且命题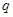 假,求
假,求 的取值范围。
的取值范围。 ,q:关于x的不等式x2-4x+m2≤0的解集是空集,试确定实数m的取值范围,使得p或q为真命题,p且q为假命题
,q:关于x的不等式x2-4x+m2≤0的解集是空集,试确定实数m的取值范围,使得p或q为真命题,p且q为假命题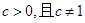 ,设
,设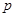 :函数
:函数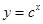 在
在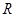 上单调递减;
上单调递减;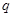 :函数
:函数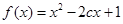 在
在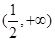 上为增函数.
上为增函数.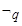 为假,求实数
为假,求实数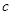 的取值范围;
的取值范围; ”为假,“
”为假,“ 表示双曲线,命题
表示双曲线,命题 表示椭圆.
表示椭圆. 为真命题,求实数
为真命题,求实数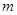 的取值范围.
的取值范围. 为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和 “既不充分也不必要条件”中的哪一个).
为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和 “既不充分也不必要条件”中的哪一个). 满足
满足 (其中
(其中 ),命题q:实数
),命题q:实数
 ,且
,且 为真,求实数
为真,求实数 的取值范围;
的取值范围; 是
是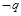 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.